题目内容
水平放置的△ABC的直观图为△A′B′C′，A′B′∥y′轴，B′C′在x′轴上，则△ABC是（ ）
分析：根据斜二测画法作平面图形的直观图的原理，可得△ABC中∠ABC=90°，得△ABC是直角三角形．
解答：解：∵在直观图中，x'o'y'坐标系所成角为45°，
∴由A′B′∥y′轴，B′C′在x′轴上，得∠A′B′C'=45°或135°
∵直观图中，x'o'y'坐标系所成角角是90°角的直观图
∴∠ABC=90°，可得△ABC是直角三角形
故选：C
∴由A′B′∥y′轴，B′C′在x′轴上，得∠A′B′C'=45°或135°
∵直观图中，x'o'y'坐标系所成角角是90°角的直观图
∴∠ABC=90°，可得△ABC是直角三角形
故选：C
点评：本题给出三角形的直观图的形状，判断三角形原来的形状，着重考查了斜二测画法作平面图形的直观图和三角形形状的判断等知识，属于基础题．
练习册系列答案
相关题目
水平放置的△ABC的斜二测直观图如图所示，已知A′C′=3，B′C′=2，则AB边上的中线的实际长度为
如图，△A′B′C′是水平放置的△ABC的斜二测直观图，其中O′C′=O′A′=1，O′B′=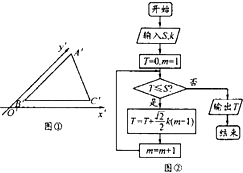
如图①，利用斜二侧画法得到水平放置的△ABC的直观图△A′B′C′，其中A′B′∥y′轴，B′C′∥x′轴．若A′B′=B′C′=3，设△ABC的面积为S，△A′B′C的面积为S′，记S=kS′，执行如图②的框图，则输出T的值（ ）