题目内容
已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为
的正三角形,则原△ABC的面积为
.
| 2 |
| 6 |
| 6 |
分析:作出图形,由图形求出点A到O'的距离,即可得到在平面图中三角形的高,再求面积即可
解答: 解:如下图,在直观图中,有正三角形A′B′C′,其边长为
解:如下图,在直观图中,有正三角形A′B′C′,其边长为
,故点A到底边BC的距离是
×
=
,作AD⊥X′于D,则△ADO′是等腰直角三角形,故可得O'A′=
,
由此可得在平面图中三角形的高为 2
,
原△ABC的面积为
×2
×
=
故答案为:
 解:如下图,在直观图中,有正三角形A′B′C′,其边长为
解:如下图,在直观图中,有正三角形A′B′C′,其边长为| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
由此可得在平面图中三角形的高为 2
| 3 |
原△ABC的面积为
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
故答案为:
| 6 |
点评:本题考查平面图形的直观图,解本题的关键是根据直观图的作图规则得出平面图的数据,并用公式求面积,此是对直观图进行考查的常见题型,应掌握把握其作题规律.

练习册系列答案
相关题目
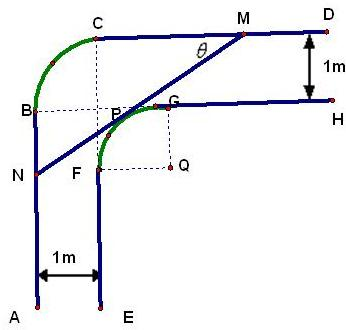 一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m. 如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知
如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知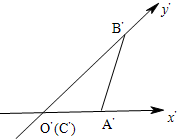 水平放置的△ABC斜二测直观图如图所示,已知A′C′=3,B′C′=2,则△ABC中AB边上中线的实际长度为
水平放置的△ABC斜二测直观图如图所示,已知A′C′=3,B′C′=2,则△ABC中AB边上中线的实际长度为 水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为
水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为