题目内容
【题目】已知函数![]() ,若存在实数
,若存在实数![]() ,使得对于定义域内的任意实数
,使得对于定义域内的任意实数![]() ,均有
,均有![]() 成立,则称函数
成立,则称函数![]() 为“可平衡”函数,有序数对
为“可平衡”函数,有序数对![]() 称为函数
称为函数![]() 的“平衡”数对.
的“平衡”数对.
(1)若![]() ,判断
,判断![]() 是否为“可平衡”函数,并说明理由;
是否为“可平衡”函数,并说明理由;
(2)若![]() ,
,![]() ,当
,当![]() 变化时,求证:
变化时,求证:![]() 与
与![]() 的“平衡”数对相同;
的“平衡”数对相同;
(3)若![]() ,且
,且![]() 、
、![]() 均为函数
均为函数![]() 的“平衡”数对.当
的“平衡”数对.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 是“可平衡”函数,详见解析(2)证明见解析(3)
是“可平衡”函数,详见解析(2)证明见解析(3)![]()
【解析】
(1)利用两角和差的正弦公式求解即可.
(2)根据题意可知,对于任意实数![]() ,
,![]() ,再列式利用恒成立问题求解即可.
,再列式利用恒成立问题求解即可.
(3)根据“平衡数对”的定义将![]() 用关于
用关于![]() 的三角函数表达,再利用三角函数的取值范围求解即可.
的三角函数表达,再利用三角函数的取值范围求解即可.
(1)若![]() ,则
,则![]() ,
,
![]()
![]() ,
,
要使得![]() 为“可平衡”函数,需使故
为“可平衡”函数,需使故![]() 对于任意实数
对于任意实数![]() 均成立,只有
均成立,只有![]() ,
,
此时![]() ,
,![]() ,故
,故![]() 存在,所以
存在,所以![]() 是“可平衡”函数.
是“可平衡”函数.
(2)![]() 及
及![]() 的定义域均为
的定义域均为![]() ,
,
根据题意可知,对于任意实数![]() ,
,![]() ,
,
即![]() ,即
,即![]() 对于任意实数
对于任意实数![]() 恒成立,
恒成立,
只有![]() ,
,![]() ,故函数
,故函数![]() 的“平衡”数对为
的“平衡”数对为![]() ,
,
对于函数![]() 而言,
而言,![]()
![]() ,
,
所以![]() ,
,
![]() ,
,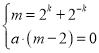 ,
,
即![]() ,故
,故![]() ,只有
,只有![]() ,所以函数
,所以函数![]() 的“平衡”数对为
的“平衡”数对为![]() ,
,
综上可得函数![]() 与
与![]() 的“平衡”数对相同.
的“平衡”数对相同.
(3)![]() ,所以
,所以![]() ,
,
![]() ,所以
,所以![]() ,
,
由于![]() ,所以
,所以![]() ,故
,故![]() ,
,![]() ,
,
![]()
![]() ,
,
由于![]() ,所以
,所以![]() 时,
时,![]() ,
,
![]() ,所以
,所以![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目