题目内容
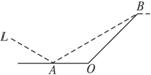
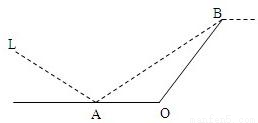
某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km, 问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.
问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.
同下
解析:
△AOB中,设OA=a,OB=b.因为AO为正西方向,OB为东北方向,故∠AOB=135°.
则|AB|2=a2+b2-2abcos135°=a2+b2+![]() ab ……………………(3分)
ab ……………………(3分)
≥2ab+![]() ab=(2+
ab=(2+![]() )ab, ……………………(6分)
)ab, ……………………(6分)
又![]() ,
,
![]() , ………………………(9分)
, ………………………(9分)
![]() ,
,![]() , ……………………(12分)
, ……………………(12分)
当![]() 时,取等号 ………………………(14分)
时,取等号 ………………………(14分)
所以把A、B分别设在公路上离中心O都是![]() Km才能使|AB|最短,其最短距离为
Km才能使|AB|最短,其最短距离为![]() Km …………………(15分)
Km …………………(15分)

练习册系列答案
相关题目
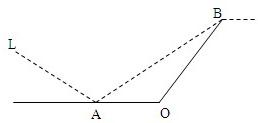 某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.
某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.