Question

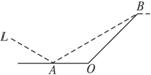
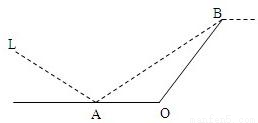
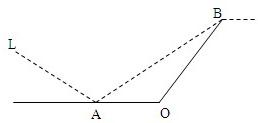某城市有一条公路，自西向东经过A点到市中心O点后转向东北方向OB，现要修建一条铁路L，L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，现要求市中心O与AB的距离为10 km，问把A、B分别设在公路上离中心O多远处才能使|AB|最短？并求其最短距离．

Answer 1

分析：设OA=a，OB=b．进而根据题意求得∠AOB，则利用余弦定理求得AB的范围，进而表示出三角形的面积求得ab和AB的关系，进而判断出把A、B分别设在公路上离中心O能使|AB|最短．

解答：解：在△AOB中，设OA=a，OB=b．
因为AO为正西方向，OB为东北方向，
所以∠AOB=135°．
则|AB|²=a²+b²-2abcos135°=a²+b²+

2

ab
≥2ab+

2

ab=（2+

2

）ab，
又

1

2

•|AB|•10=

1

2

absin1350，
∴ab=10

2

|AB|，
∴|AB|2≥10

2

(2+

2

)|AB|，
∴|AB|≥20(

2

+1)，
当a=b=10

4+2 2

时，取等号
所以把A、B分别设在公路上离中心O都是10

4+2 2

Km才能使|AB|最短，
其最短距离为20(

2

+1)Km．

点评：本题主要考查了解三角形的实际应用．解题的关键是求得ab和AB的关系．