题目内容
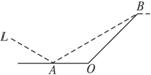
某城市有一条公路自西向东通过市中心O后转向东北方向OB,现要修建一条铁路L,并在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短,并求出最短距离.
解:在△AOB中,设OA=a,OB=b,
∵AO为正东方向,OB为东北方向,
∴∠AOB=135°.
∴|AB|2=a2+b2-2abcos135°=a2+b2+![]() ab.
ab.
又O到AB的距离为10,
设∠OAB=α(0°<α<45°),
则∠OBA=45°-α.
∴a=![]() ,b=
,b=![]() .∴|AB|2=
.∴|AB|2=![]() +
+![]() +
+![]() ·
·![]() ·
·![]() =
=
100·![]() =
=![]()
=![]() =
=![]() .
.
∴0°<α<45°,
∴45°<2α+45°<135°.
∴![]() <sin(2α+45°)≤1.
<sin(2α+45°)≤1.
∴|AB|2≥![]() =400(
=400(![]() +1)2(当且仅当α=22.5°时取等号).
+1)2(当且仅当α=22.5°时取等号).
∴|AB|min=20(![]() +1).
+1).
此时,a=b=![]() =10
=10![]() ,
,
即当A、B离O点均为10![]() km时,能使|AB|最短.其最短距离为20(
km时,能使|AB|最短.其最短距离为20(![]() +1) km.
+1) km.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
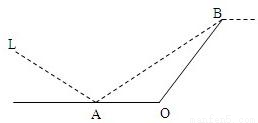
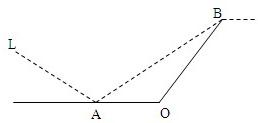 某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.
某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离. 问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.
问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.