题目内容
(1)若
=3,tan(α-β)=2,求tan(β-2α)的值;
(2)已知sin(3π+θ)=
,求
+
.
| sinα+cosα |
| sinα-cosα |
(2)已知sin(3π+θ)=
| 1 |
| 3 |
| cos(π+θ) |
| cosθ[cos(π-θ)-1] |
| cos(θ-2π) | ||||
sin(θ-
|
(1)若
=3,则有
=3,解得 tanα=2.
又tan(α-β)=2,∴tan(β-α)=-2,
∴tan(β-2α)=tan[(β-α)-α]=
=
=
.
(2)∵已知sin(3π+θ)=
=-sinθ,∴sinθ=-
.
∴
+
=
+
=
+
=
+
=
=
=18.
| sinα+cosα |
| sinα-cosα |
| tanα+1 |
| tanα-1 |
又tan(α-β)=2,∴tan(β-α)=-2,
∴tan(β-2α)=tan[(β-α)-α]=
| tan(β-α)-tanα |
| 1+tan(β-α)tanα |
| -2-2 |
| 1+(-2)×2 |
| 4 |
| 3 |
(2)∵已知sin(3π+θ)=
| 1 |
| 3 |
| 1 |
| 3 |
∴
| cos(π+θ) |
| cosθ[cos(π-θ)-1] |
| cos(θ-2π) | ||||
sin(θ-
|
| -cosθ |
| cosθ•(-cosθ-1) |
| cosθ | ||
-sin(
|
=
| 1 |
| 1+cosθ |
| cosθ |
| -cos2θ+cosθ |
| 1 |
| 1+cosθ |
| 1 |
| 1-cosθ |
| 2 |
| 1-cos2θ |
| 2 |
| sin2θ |

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
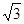 ,且c =
,且c =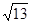 ,C =
,C =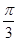 ,求a,b的值
,求a,b的值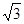 ,且c =
,且c =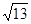 ,C =
,C =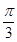 ,求a,b的值.
,求a,b的值.