题目内容
口袋中有大小、形状都相同的2只白球和1只黑球,先摸出1只球,记下颜色后放回口袋,然后再摸出1只球,则出现“两次摸出的球颜色相同”的概率是
.
| 5 |
| 9 |
| 5 |
| 9 |
分析:本题是一个有放回抽取的概率模型,故每次抽取时出现在同种颜色的球的概率是不变的,事件“两次摸出的球颜色相同”包括了两次摸出的都是黑球与都是白球两种情况,分别计算出它们发生的概率,求和既得答案
解答:解:若两次抽取的球都是黑球,则它发生的概率是
×
=
若两次抽取的球都是白球,则它发生的概率是
×
=
所以事件“两次摸出的球颜色相同”的概率是
+
=
故答案为
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
若两次抽取的球都是白球,则它发生的概率是
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
所以事件“两次摸出的球颜色相同”的概率是
| 1 |
| 9 |
| 4 |
| 9 |
| 5 |
| 9 |
故答案为
| 5 |
| 9 |
点评:本题考查相互独立事件的概率乘法公式,解题的关键是理解事件“两次摸出的球颜色相同”,本题的难点是理解事件两球颜色相同的抽取方法,能从中抽象出两次抽取之间是一个相互独立事件.

练习册系列答案
相关题目
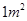 的正方形内,求球落在正方形内切圆内的概率;
的正方形内,求球落在正方形内切圆内的概率;