题目内容
口袋中有大小、形状都相同的七个球,其中白球3个,红球4个,(1)任取一个球投在一个面积为1m2的正方形内,求球落在正方形内切圆内的概率;
(2)若在袋中任取两个,求取到红球的概率.
【答案】分析:(1)正方形的边长为1,则内切圆半径为 ,然后求出正方形面积及其内切圆的面积,代入几何概型公式,即可得到答案.
,然后求出正方形面积及其内切圆的面积,代入几何概型公式,即可得到答案.
(1)从甲口袋中摸出的2个球,利用组合算出所有的事件,共有C72个,都是白球的有:C32,利用概率公式计算两个都为白球的概率,最后根据彼此互斥概率公式得到结果即可.
解答: 解:(1)正方形内切圆半径
解:(1)正方形内切圆半径 ,内切圆面积为
,内切圆面积为 ,
,
设“落在圆内”为事件A,
则 ….(4分)
….(4分)
(2)设“取到红球”为事件A则 为“两个都为白球”…(5分)
为“两个都为白球”…(5分)
实验“在袋中任取两个”共有基本事件C72=21个,…(7分)
“两个都为白球”包含C32=3个基本事件,…(8分)
所以P( )=
)= ,
,
P(A)= …(10分)
…(10分)
点评:本题主要考查了古典概型、几何概型,互斥事件的概率公式,以及圆与正方形的面积的计算,解题的关键是弄清概率类型,属于中档题.
 ,然后求出正方形面积及其内切圆的面积,代入几何概型公式,即可得到答案.
,然后求出正方形面积及其内切圆的面积,代入几何概型公式,即可得到答案.(1)从甲口袋中摸出的2个球,利用组合算出所有的事件,共有C72个,都是白球的有:C32,利用概率公式计算两个都为白球的概率,最后根据彼此互斥概率公式得到结果即可.
解答:
 解:(1)正方形内切圆半径
解:(1)正方形内切圆半径 ,内切圆面积为
,内切圆面积为 ,
,设“落在圆内”为事件A,
则
 ….(4分)
….(4分)(2)设“取到红球”为事件A则
 为“两个都为白球”…(5分)
为“两个都为白球”…(5分)实验“在袋中任取两个”共有基本事件C72=21个,…(7分)
“两个都为白球”包含C32=3个基本事件,…(8分)
所以P(
 )=
)= ,
,P(A)=
 …(10分)
…(10分)点评:本题主要考查了古典概型、几何概型,互斥事件的概率公式,以及圆与正方形的面积的计算,解题的关键是弄清概率类型,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
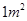 的正方形内,求球落在正方形内切圆内的概率;
的正方形内,求球落在正方形内切圆内的概率;