题目内容
【题目】设正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若正项等比数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意
,若对任意![]() ,均有
,均有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)an=2n;(Ⅱ)[![]() ,+∞).
,+∞).
【解析】
(Ⅰ)对递推关系![]() 再递推一步,两式相减,最后结合等差数列的定义进行求解即可;
再递推一步,两式相减,最后结合等差数列的定义进行求解即可;
(Ⅱ)根据等差数列的通项公式结合已知求出等比数列的通项公式,最后利用错位相减法、判断数列的单调性进行求解即可.
(Ⅰ)因为![]() ,所以
,所以![]() (n≥2),
(n≥2),
两式相减得:an+12﹣an2=4an+4,即an+12=(an+2)2(n≥2),
又因为数列{an}的各项均为正数,所以an+1=an+2(n≥2),
又因为a2=4,16=a12+4+4,可得a1=2,
所以当n=1时上式成立,即数列{an}是首项为2、公差为2的等差数列,
所以![]() ;
;
(Ⅱ)由(1)可知b1=a1=2,b3=a4=8,所以正项等比数列![]() 的公比为:
的公比为:![]() ,
,
因此bn=![]() ;cn=
;cn=![]() .
.
![]() ①
①
![]() ②
②
① —②得:
![]()
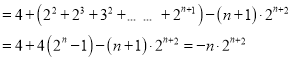
![]()
![]() 恒成立,等价于
恒成立,等价于![]() 恒成立,
恒成立,
所以![]() 恒成立,
恒成立,
设kn=![]() ,则kn+1﹣kn=
,则kn+1﹣kn=![]() ﹣
﹣![]() =
=![]() ,
,
所以当n≤4时kn+1>kn,当n>4时kn+1<kn,
所以![]()
所以当kn的最大值为k5=![]() ,故m≥
,故m≥![]() ,
,
即实数m的取值范围是:[![]() ,+∞).
,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目