题目内容
如图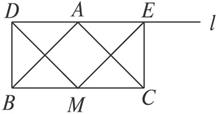
图
解析:特别地,当l∥BC时,四边形BCED是矩形,容易看出△ABC≌△MED,△DME是等腰直角三角形.
因此我们猜想当l与BC不平行时结论仍然成立.
即△DME是等腰直角三角形.
证明:过M作MF∥CE,可证MF是梯形BCED中位线.
∴MF=![]() (BD+CE).
(BD+CE).
又由△ADB≌△CEA,∴BD+CE=DA+AE,即MF=![]() DE.∴△DME是直角三角形.
DE.∴△DME是直角三角形.
又MF⊥DE,FD=FE,∴ME=MD.
∴△DME是等腰直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目