题目内容
求适合下列条件的曲线的标准方程:
(1)a=6,c=3,焦点在y轴上的椭圆
(2)过点M(
,1),且焦点为F1(-
,0)的椭圆
(3)一条渐近线方程是3x+4y=0,一个焦点是(5,0)的双曲线.
(1)a=6,c=3,焦点在y轴上的椭圆
(2)过点M(
| 2 |
| 2 |
(3)一条渐近线方程是3x+4y=0,一个焦点是(5,0)的双曲线.
分析:(1)先求出b,再注意到焦点在y轴上,写出椭圆方程即可.
(2)由已知,得出另一焦点F2(
,0),c=
,根据椭圆的定义,2a=|MF1|+|MF2|,求出a,b,得出椭圆方程.
(3)由已知,得出
解出a,b后可得出双曲线方程
(2)由已知,得出另一焦点F2(
| 2 |
| 2 |
(3)由已知,得出
|
解答:解:(1)a=6,c=3,∴b2=a2-c2=27,又焦点在y轴上∴方程为
+
=1.
(2)由已知,得出另一焦点F2(
,0),c=
,
根据椭圆的定义,2a=|MF1|+|MF2|=4,a=2,∴b2=a2-c2=2,
又焦点在x轴上,
∴方程为
+
=1
(3)一条渐近线方程是3x+4y=0,即y=-
x,一个焦点是(5,0)
∴
解得a=4,b=3,双曲线方程为
-
=1
| y2 |
| 36 |
| x2 |
| 27 |
(2)由已知,得出另一焦点F2(
| 2 |
| 2 |
根据椭圆的定义,2a=|MF1|+|MF2|=4,a=2,∴b2=a2-c2=2,
又焦点在x轴上,
∴方程为
| x2 |
| 4 |
| y2 |
| 2 |
(3)一条渐近线方程是3x+4y=0,即y=-
| 3 |
| 4 |
∴
|
解得a=4,b=3,双曲线方程为
| x2 |
| 16 |
| y2 |
| 9 |
点评:本题考查椭圆、双曲线的定义、简单几何性质、标准方程求解.对基础知识准确掌握并灵活应用是此类问题解决的途径.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
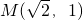 ,且焦点为
,且焦点为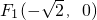 的椭圆
的椭圆 ,且焦点为
,且焦点为 的椭圆
的椭圆