题目内容
已知定点A(12.0),M为曲线
|
| AP |
| AM |
分析:先设M(6+2cosθ,2sinθ),动点(x,y),根据
=2
可得M为线段AP的中点,再根据中点坐标公式建立等量关系即可求出轨迹方程.
| AP |
| AM |
解答:解:设M(6+2cosθ,2sinθ),动点(x,y)
由
=2
,即M为线段AP的中点
故6+2cosθ=
,2sinθ=
即
即x2+y2=16
∴动点P的轨迹C的方程为x2+y2=16
由
| AP |
| AM |
故6+2cosθ=
| x+12 |
| 2 |
| y+0 |
| 2 |
即
|
∴动点P的轨迹C的方程为x2+y2=16
点评:本题主要考查了圆的参数方程,以及中点坐标公式的应用,同时考查了共线向量等有关知识,属于基础题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 上的动点,若
上的动点,若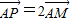 ,试求动点P的轨迹C的方程.
,试求动点P的轨迹C的方程.