题目内容
若正数项数列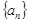 的前
的前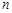 项和为
项和为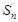 ,首项
,首项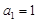 ,点
,点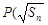 ,
,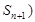 在曲线
在曲线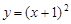 上.
上.
(1)求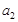 ,
,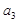 ;
;
(2)求数列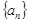 的通项公式
的通项公式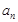 ;
;
(3)设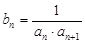 ,
,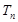 表示数列
表示数列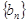 的前项和,若
的前项和,若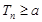 恒成立,求
恒成立,求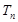 及实数
及实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:(1)根据已知点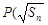 ,
,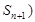 在曲线
在曲线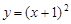 上,代入曲线,得到
上,代入曲线,得到 与
与 的关系,再根据
的关系,再根据 ,分别取
,分别取 和
和 代入关系式,得到关于
代入关系式,得到关于 与
与 的方程组,解方程,得到结果;(2)由(1)得的
的方程组,解方程,得到结果;(2)由(1)得的 ,因为是正项数列,所以两边开方,得
,因为是正项数列,所以两边开方,得 与
与 的地推关系式,从而判定数列形式,得出
的地推关系式,从而判定数列形式,得出 的通项公式,再根据
的通项公式,再根据
 ,得出
,得出 的通项公式;(3)代入
的通项公式;(3)代入 的通项公式得到
的通项公式得到 ,然后裂项,经过裂项相消,得到
,然后裂项,经过裂项相消,得到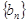 的前项和
的前项和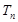 ,,通过分离常数可以判定
,,通过分离常数可以判定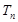 的单调性,求出最值,若
的单调性,求出最值,若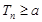 恒成立,那么
恒成立,那么 ,得到的范围.此题计算相对较大,属于中档题.
,得到的范围.此题计算相对较大,属于中档题.
试题解析:(1)解:因为点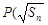 ,
,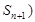 在曲线
在曲线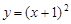 上,所以
上,所以 .
.
分别取 和
和 ,得到
,得到 ,
,
由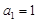 解得
解得 ,
, . 4分
. 4分
(2)解:由 得
得 .
.
数列 是以
是以 为首项,
为首项, 为公差的等差数列,所以
为公差的等差数列,所以 , 6分
, 6分
由
 ,当
,当 时,
时, ,
,
所以 . 8分
. 8分
(3)解:因为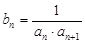

 ,
,
所以

 , 11分
, 11分
显然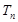 是关于
是关于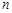 的增函数, 所以
的增函数, 所以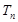 有最小值
有最小值 ,
,
因为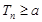 恒成立,所以
恒成立,所以 ,
,
因此 ,实数
,实数 的取值范围是
的取值范围是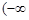 ,
, . 13分
. 13分
考点:1.等差数列的定义;2.已知 求
求 ;3.裂项相消;4.函数最值.
;3.裂项相消;4.函数最值.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
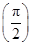 =0.
=0.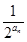 ),求数列{bn}的前n项和Sn.
),求数列{bn}的前n项和Sn.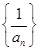 是等差数列并求数列{an}的通项公式;
是等差数列并求数列{an}的通项公式;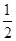 .
.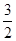 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列. (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值. 的首项
的首项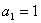 ,前
,前 项和为
项和为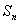 (
(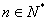 ),且点
),且点 在直线
在直线 上(
上(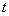 为与
为与 )为等比数列;
)为等比数列;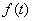 ,数列
,数列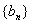 满足
满足 ,设
,设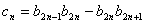 ,求数列
,求数列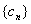 的前
的前 ;
;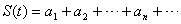 ,求函数
,求函数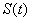 的值域.
的值域.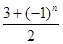 ,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n, .
.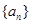 的前
的前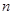 项和为
项和为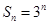 ,数列
,数列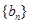 满足:
满足: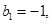
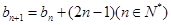 。
。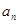 ;
;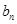 ;
;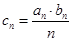 ,求数列
,求数列 的前
的前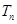 .
.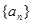 是公差不为零的等差数列,
是公差不为零的等差数列,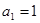 ,且
,且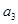 是
是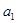 和
和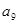 的等比中项.
的等比中项.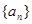 的通项公式;
的通项公式;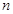 项和为
项和为 ,
,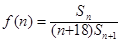 ,试问当
,试问当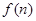 最大?并求出
最大?并求出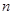 个月月底余
个月月底余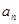 元,第
元,第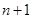 个月月底余
个月月底余 元,写出
元,写出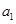 的值并建立
的值并建立