Question

【题目】设各项均为整数的无穷数列满足：，且对所有，均成立.

（1）写出的所有可能值（不需要写计算过程）；

（2）若是公差为1的等差数列，求的通项公式；

（3）证明：存在满足条件的数列，使得在该数列中，有无穷多项为2019.

Answer 1

【答案】（1），，，1，3，5，7；（2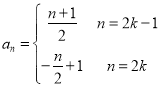），；（3）证明见解析.

【解析】

（1）通过列举法表示出所有可能值

（2）分析可知表示的是原数列中的奇数项，求得奇数项的通项公式，再利用相邻两项差的绝对值的关系构造关系式解出偶数项，进而求得通项

（3）可利用（2）中的数列，构造一个循环数列，则可证明循环数列中存在无穷多项为2019

（1），，，1，3，5，7；

（2）是公差为1的等差数列，

数列的所有奇数项为公差为1的等差数列，

当时，

当时，由可知：，即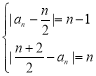

解得：，；

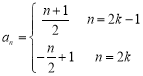（3）由（2）可知存在一个数列使得奇数项为从1开始的连续自然数，则易知，

然后自4037项开始，构造奇数项为公差为的等差数列，由（2）可知，

当，时，

当时，由可知

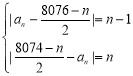即，解得：

则当奇数项取至1时，重复第一段的数列，得到一个周期数列，在此周期数列中，存在无穷多项为2019，即可得证．