题目内容
已知 .
.
(1)求f(x)的定义域、值域;
(2)若f(x)=2, ,求x的值.
,求x的值.
解: (4分)
(4分)
(1)因为1+sin2x≠0所以sin2x≠-1,2x≠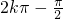 (k∈Z),x≠
(k∈Z),x≠ (k?Z).
(k?Z).
又0<1+sin2x≤2,所以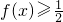 .
.
所以定义域为{x|x≠ ,k∈Z},值域为:{y|y≥
,k∈Z},值域为:{y|y≥ }(4分)
}(4分)
(2)因为f(x)=2,所以 ,
,
因为 所以
所以
所以 或
或
所以 或
或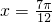 (6分)
(6分)
分析:(1)先利用三角函数公式得 ;再利用分母不为0求出定义域,利用正弦函数的函数值求出函数的值域;
;再利用分母不为0求出定义域,利用正弦函数的函数值求出函数的值域;
(2)由f(x)=2,所以 ,
, ,再利用
,再利用 ,求出
,求出 ,两则相结合即可求出结果.
,两则相结合即可求出结果.
点评:本题主要考查三角函数中的恒等变换应用以及正弦函数的定义域和值域和利用正弦函数的单调性求值.在求函数定义域时,如果原题中带分母,一定注意分母不为0.
 (4分)
(4分)(1)因为1+sin2x≠0所以sin2x≠-1,2x≠
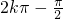 (k∈Z),x≠
(k∈Z),x≠ (k?Z).
(k?Z).又0<1+sin2x≤2,所以
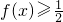 .
.所以定义域为{x|x≠
 ,k∈Z},值域为:{y|y≥
,k∈Z},值域为:{y|y≥ }(4分)
}(4分)(2)因为f(x)=2,所以
 ,
,
因为
 所以
所以
所以
 或
或
所以
 或
或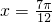 (6分)
(6分)分析:(1)先利用三角函数公式得
 ;再利用分母不为0求出定义域,利用正弦函数的函数值求出函数的值域;
;再利用分母不为0求出定义域,利用正弦函数的函数值求出函数的值域;(2)由f(x)=2,所以
 ,
, ,再利用
,再利用 ,求出
,求出 ,两则相结合即可求出结果.
,两则相结合即可求出结果.点评:本题主要考查三角函数中的恒等变换应用以及正弦函数的定义域和值域和利用正弦函数的单调性求值.在求函数定义域时,如果原题中带分母,一定注意分母不为0.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
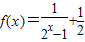
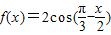
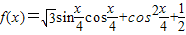 .
.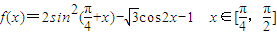
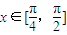 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.