题目内容
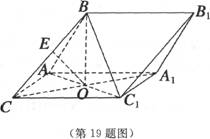
(本题满分13分)如图所示,三棱柱ABC—A1B1C1中,AB=AC=AA1=2,面ABC1上面AAlClC,∠AAlCl=∠BAC1=600,AC1与A1C相交于0,E为BC的中点.
(1)求证.OE∥面AAl BlB;
(2)求证:B0⊥面AA1C1C;
(3)求三棱锥C—AEC1的体积.
【答案】
 (1)证明:连
(1)证明:连 在
在 中,E,O分别为BC和CA1的中点,
中,E,O分别为BC和CA1的中点,
∴

∴ …………………………4分
…………………………4分
(2)由条件知,四边形ACC1A1为菱形
∠AA1C1=60°,∴A1C=2 ,ΔABC1中,AB=2, ,∴BC1=2,又
,∴BC1=2,又 的中点
的中点
∴BO⊥AC1 ,又平面 ,
,
∴ ………………………………… 9分
………………………………… 9分
(3)∵ ,取OC的中点F,连接EF,则EF为三棱锥E-ACC1的高,EF=
,取OC的中点F,连接EF,则EF为三棱锥E-ACC1的高,EF= OB=
OB= ,∴
,∴

………………………………… 13分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在城
在城 的南偏西
的南偏西 的方向上,由
的方向上,由 ,在
,在 处,有一人正沿公路向
处,有一人正沿公路向 处,此时
处,此时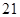 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达
 中,
中, ,
, ,
, ,
, ,
, ,
, 是
是 的中点,设
的中点,设 ,
, ,
, .
.
 表示
表示 ;
; 的长.
的长.
 ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD,  ,O为AD中点.
,O为AD中点.
 与平面
与平面 所成角的余弦值;
所成角的余弦值; 点到平面
点到平面 的距离
的距离 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 中,已知
中,已知
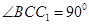 ,
,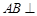 侧面
侧面

 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).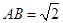 ,求二面角
,求二面角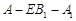 的大小.
的大小.