题目内容
(本题满分13分)如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′—EC—B是直二面角.

(1)证明:BE⊥C D′;
(2)求二面角D′—BC—E的正切值.
【答案】
(1)见解析;
(2)
【解析】解:(1)∵AD=2AB=2,E是AD的中点,
∴△BAE,△CDE是等腰直角三角形,
易知, ∠BEC=90°,即BE⊥EC.
又∵平面D′EC⊥平面BEC,面D′EC∩面BEC=EC,
∴BE⊥面D′EC,又C D′Ì 面D′EC , ∴BE⊥CD′;
(2)法一:设M是线段EC的中点,过M作MF⊥BC垂足为F,连接D′M,D′F,则D′M⊥EC.

∵平面D′EC⊥平面BEC,
∴D′M⊥平面EBC,
∴MF是D′F在平面BEC上的射影,由三垂线定理得:
D′F⊥BC
∴∠D′FM是二面D′—BC—E的平面角.
在Rt△D′MF中,D′M= EC=
EC= ,MF=
,MF= AB=
AB=
∴
即二面角D′—BC—E的正切值为 .
.
法二:如图,以EB,EC为x轴、y轴,过E垂直于平面BEC的射线为z轴,建立空间直角坐标系.

则B( ,0,0),C(0,
,0,0),C(0, ,0),D′(0,
,0),D′(0, ,
, )
)
设平面BEC的法向量为 ;平面D′BC的法向量为
;平面D′BC的法向量为

Þ tan =
=
 ∴二面角D′—BC—E的正切值为
∴二面角D′—BC—E的正切值为 .
.

练习册系列答案
相关题目
 在城
在城 的南偏西
的南偏西 的方向上,由
的方向上,由 ,在
,在 处,有一人正沿公路向
处,有一人正沿公路向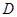 处,此时
处,此时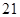 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达
 中,
中,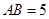 ,
, ,
, ,
, ,
, ,
, 是
是 的中点,设
的中点,设 ,
, ,
, .
.
 表示
表示 ;
; 的长.
的长. ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD,  ,O为AD中点.
,O为AD中点.
 与平面
与平面 所成角的余弦值;
所成角的余弦值; 点到平面
点到平面 的距离
的距离 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 中,已知
中,已知
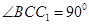 ,
,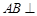 侧面
侧面

 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).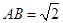 ,求二面角
,求二面角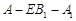 的大小.
的大小.