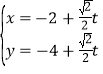题目内容
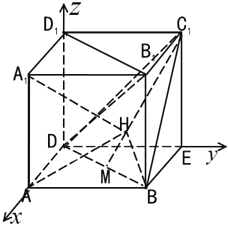
【题目】如图,在多面体ABD﹣A1B1C1D1中四边形A1B1C1D1,ADD1A1.ABB1A1均为正方形.点M是BD的中点.点H在线段C1M上,且A1H与平面ABD所成角的正弦值为![]() .
.
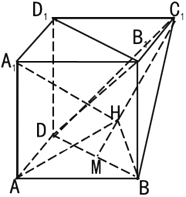
(Ⅰ)证明:B1D1∥平面BC1D:
(Ⅱ)求二面角A﹣A1H﹣B的的正弦值.
【答案】(Ⅰ)证明见解析 (Ⅱ)![]() .
.
【解析】
(Ⅰ)构造正方体证明BD∥B1D1即可.
(Ⅱ)建立空间直角坐标系,利用A1H与平面ABD所成角的正弦值为![]() 可求得
可求得![]() 的坐标,再利用空间向量求二面角的方法求解即可.
的坐标,再利用空间向量求二面角的方法求解即可.
(Ⅰ)证明:如图,构造正方体ABED﹣A1B1C1D1,
结合正方体ABED﹣A1B1C1D1,得BD∥B1D1,
∵BD平面BC1D,B1D1平面BC1D,
∴B1D1∥平面BC1D.
(Ⅱ)解:以D为原点,DA为x轴,DE为y轴,DD1为z轴,建立空间直角坐标系,
设AD=2,则M(1,1,0),C1(0,2,2),A1(2,0,2),A(2,0,0),B(2,2,0),
设H(a,b,c),![]() ,(0≤λ≤1),则(a,b﹣2,c﹣2)=(λ,﹣λ,﹣2λ),
,(0≤λ≤1),则(a,b﹣2,c﹣2)=(λ,﹣λ,﹣2λ),
∴H(λ,2﹣λ,2﹣2λ),
平面ABD的法向量![]() (0,0,1),
(0,0,1),![]() (λ﹣2,2﹣λ,﹣2λ),
(λ﹣2,2﹣λ,﹣2λ),
∵A1H与平面ABD所成角的正弦值为![]() .
.
∴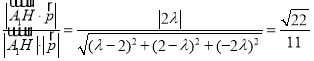 ,
,
解得![]() ,(舍负),∴H(
,(舍负),∴H(![]() ,
,![]() ,1),
,1),
![]() (
(![]() ,
,![]() ,﹣1),
,﹣1),![]() (0,0,﹣2),
(0,0,﹣2),![]() (0,2,﹣2),
(0,2,﹣2),
设平面AA1H的法向量![]() (x,y,z),
(x,y,z),
则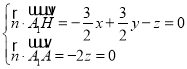 ,取x=1,得
,取x=1,得![]() (1,1,0),
(1,1,0),
设平面A1HB的法向量![]() (x,y,z),
(x,y,z),
则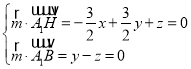 ,取y=1,得
,取y=1,得![]() (
(![]() ,1,1),
,1,1),
设二面角A﹣A1H﹣B的平面角为θ,
则cosθ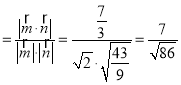 ,
,
∴二面角A﹣A1H﹣B的正弦值为:
sinθ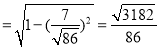 .
.

【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度![]() (单位:cm)的情况如表1:
(单位:cm)的情况如表1:
| 900 | 700 | 300 | 100 |
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年11月份AQI指数频数分布如表2:
|
|
|
|
|
|
频数(天) | 3 | 6 | 12 | 6 | 3 |
<>(1)设
(2)小李在该市开了一家洗车店,洗车店每天的平均收入与AQI指数存在相关关系如表3:
|
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
根据表3估计小李的洗车店2017年11月份每天的平均收入.
附参考公式:![]() ,其中
,其中 ,
,![]() .
.
【题目】(1)某校夏令营有3名男同学A、B、C和3名女同学X、Y、Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
①用表中字母列举出所有可能的结果;
②设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
(2)节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是多少?