题目内容
【题目】设二阶方矩阵![]() ,则矩阵
,则矩阵![]() 所对应的矩阵变换为:
所对应的矩阵变换为:![]() ,其意义是把点
,其意义是把点![]() 变换为点
变换为点![]() ,矩阵
,矩阵![]() 叫做变换矩阵.
叫做变换矩阵.
(1)当变换矩阵![]() 时,点
时,点![]() 、
、![]() 经矩阵变换后得到点分别是
经矩阵变换后得到点分别是![]() 、
、![]() ,求经过点
,求经过点![]() 、
、![]() 的直线的点方向式方程;
的直线的点方向式方程;
(2)当变换矩阵![]() 时,若直线上的任意点
时,若直线上的任意点![]() 经矩阵变换后得到的点
经矩阵变换后得到的点![]() 仍在该直线上,求直线的方程;
仍在该直线上,求直线的方程;
(3)若点![]() 经过矩阵
经过矩阵![]() 变换后得到点
变换后得到点![]() ,且
,且![]() 与
与![]() 关于直线
关于直线![]() 对称,求变换矩阵
对称,求变换矩阵![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3) .
.
【解析】
(1)由给出的变换矩阵定义求出![]() 、
、![]() 的坐标,进而求出直线的方向向量,求出点向式方程;
的坐标,进而求出直线的方向向量,求出点向式方程;
(2)设直线方程为:![]() :
:![]() ,求出其上点
,求出其上点![]() 关于矩阵
关于矩阵![]() 变换后的点
变换后的点![]() 也满足直线
也满足直线![]() 的方程,再根据两直线重合的条件:斜率相等,截距相同即可求出直线方程;
的方程,再根据两直线重合的条件:斜率相等,截距相同即可求出直线方程;
(3)因为点![]() 经过矩阵
经过矩阵![]() 变换后得到点
变换后得到点![]() ,且
,且![]() 与
与![]() 关于直线
关于直线![]() 对称,所以有:
对称,所以有:
 ,解之得:
,解之得: ,再根据
,再根据![]() ,得出
,得出![]() 即可.
即可.
(1)由题意得:![]() ,即
,即![]() ,解之得:
,解之得:![]() ,所以
,所以![]() ;
;
![]() ,即
,即![]() ,解之得:
,解之得: ,所以
,所以![]() ,
,
则![]() ,
,
所以方程为 ,即
,即![]() ;
;
(2)![]() ,即
,即![]()
 ,
,
设![]() :
:![]() (
(![]() 不全为
不全为![]() ),
),
![]() :
:![]() ,即
,即![]() ,
,
由题知,![]() 与
与![]() 重合得
重合得![]() ,
,
所以![]() 或
或![]() ,
,
![]() ,得
,得![]() ,
,
![]() ,得
,得![]() 或
或![]() ,即
,即![]() ,
,![]() ;
;
(3)因为![]() 与
与![]() 关于直线
关于直线![]() 对称,所以有:
对称,所以有:
 ,解之得:
,解之得: ,
,
故 ,所以
,所以 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】随着我国经济的飞速发展,人民生活水平得到很大提高,汽车已经进入千千万万的家庭.大部分的车主在购买汽车时,会在轿车或者![]() 中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
购买了轿车(辆) | 购买了 | |
|
|
|
|
|
|
(1)根据表,是否有![]() 的把握认为年龄与购买的汽车车型有关?
的把握认为年龄与购买的汽车车型有关?
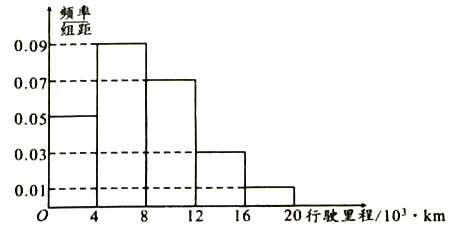
(2)图给出的是![]() 名车主上一年汽车的行驶里程,求这
名车主上一年汽车的行驶里程,求这![]() 名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
(3)用分层抽样的方法从![]() 岁以上车主中抽取
岁以上车主中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送免费保养券,求这
人赠送免费保养券,求这![]() 人中至少有
人中至少有![]() 辆轿车的概率。
辆轿车的概率。
附:![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|