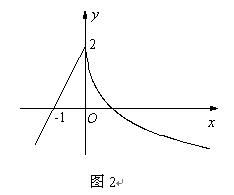
题目内容
(本题满分15分)已知直线 ,曲线
,曲线
(1)若 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数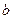 的取值;
的取值;
(2)若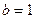 ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。
 ,曲线
,曲线
(1)若
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数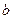 的取值;
的取值;(2)若
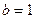 ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。解(Ⅰ)分两种情况:
1) 有惟一解,
有惟一解,
即x2 + x + b – 2 =0在(– ,
, )内有一解,
)内有一解,
由△=" 1" – 4b + 8 =" 0," 得 ,符合. 3分
,符合. 3分
2)直线过点(– ,0), 得0 = –
,0), 得0 = – + b ,得或
+ b ,得或 . 2分
. 2分
(Ⅱ)由 ,得x2 – kx – 3 =0,
,得x2 – kx – 3 =0,
则有: , 且
, 且 . 2分
. 2分
由 ,得x2 + kx –1 =0,
,得x2 + kx –1 =0,
则有: ,且kÎR.
,且kÎR.  2分
2分
所以

 2分
2分
= =
= ,且
,且 .
.
令t =" k2" ,则 ,
,
则 ,
, 是增函数,
是增函数,
所以, . 4分
. 4分
1)
 有惟一解,
有惟一解,即x2 + x + b – 2 =0在(–
 ,
, )内有一解,
)内有一解,由△=" 1" – 4b + 8 =" 0," 得
 ,符合. 3分
,符合. 3分2)直线过点(–
 ,0), 得0 = –
,0), 得0 = – + b ,得或
+ b ,得或 . 2分
. 2分(Ⅱ)由
 ,得x2 – kx – 3 =0,
,得x2 – kx – 3 =0,则有:
 , 且
, 且 . 2分
. 2分由
 ,得x2 + kx –1 =0,
,得x2 + kx –1 =0,则有:
 ,且kÎR.
,且kÎR.  2分
2分所以


 2分
2分=
 =
= ,且
,且 .
.令t =" k2" ,则
 ,
,则
 ,
, 是增函数,
是增函数,所以,
 . 4分
. 4分略

练习册系列答案
相关题目
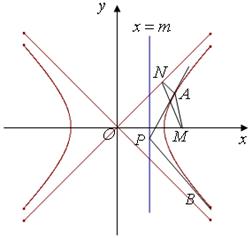
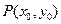 在直线
在直线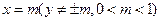 上,过点
上,过点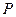 作双曲线
作双曲线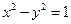 的两条切线
的两条切线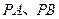 ,切点为
,切点为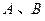 ,定点
,定点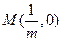 。
。
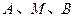 共线;
共线;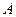 作直线
作直线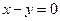 的垂线,垂足为
的垂线,垂足为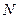 ,试求
,试求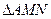 的重心
的重心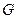 所在曲线方程。
所在曲线方程。 轴上,离心率为
轴上,离心率为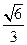 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为 ,过左准线与
,过左准线与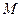 任作一条斜率不为零的直线
任作一条斜率不为零的直线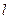 与椭圆W交于不同的两点
与椭圆W交于不同的两点 、
、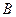 ,点
,点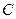 .
.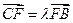 (
( );
); 面积
面积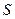 的最大值.
的最大值.  c,0)三点,其中c>0.
c,0)三点,其中c>0.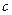 的式子表示);
的式子表示);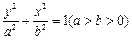 (其中
(其中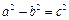 )的左、右顶点分别为D、B,
)的左、右顶点分别为D、B, 圆C:
圆C: 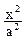 +
+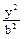 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=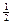 ,且椭圆经过点N(2,-3).
,且椭圆经过点N(2,-3).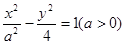 的右焦点与抛物线
的右焦点与抛物线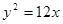 的焦点重合,则该双曲线的离心率为 ( )
的焦点重合,则该双曲线的离心率为 ( )



 与双曲线
与双曲线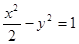 相交于
相交于 两点,则
两点,则 =_________.
=_________.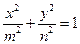 (
(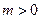 ,
,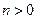 )的右焦点与抛物线
)的右焦点与抛物线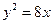 的焦点相同,离心率为
的焦点相同,离心率为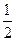 ,则此椭圆的方程为
,则此椭圆的方程为



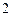 ,函数
,函数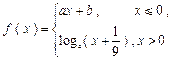 的图象是一条连续不断的曲线,则
的图象是一条连续不断的曲线,则 .
.