题目内容
7.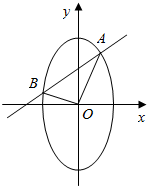 已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1,定点N(0,1),过圆M:x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点.
已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1,定点N(0,1),过圆M:x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点.(1)求证:$\overrightarrow{OA}•\overrightarrow{OB}$=0;
(2)求|AB|的取值范围.
分析 (1)当切线斜率不存在时,易得$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即OA⊥OB;当切线斜率存在时,设切线方程为y=kx+m,与椭圆方程联立消去y并由韦达定理验证$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=0即可;
(2)由(1)知当切线斜率不存在时,|AB|=$\frac{4\sqrt{5}}{5}$;当切线斜率存在时,由弦长公式可得|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|,由韦达定理和换元的思想,结合不等式的性质,可得此时|AB|的范围综合可得.
解答 (1)证明:当切线斜率不存在时,
方程为x=±$\frac{2\sqrt{5}}{5}$,
与椭圆的两个交点为($\frac{2\sqrt{5}}{5}$,±$\frac{2\sqrt{5}}{5}$)或(-$\frac{2\sqrt{5}}{5}$,±$\frac{2\sqrt{5}}{5}$),
此时有$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即OA⊥OB;
当切线斜率存在时,设切线方程为y=kx+m,
与椭圆方程联立消去y并整理可得(4+k2)x2+2kmx+m2-4=0,
由△>0可得k2-m2+4>0,设A(x1,y1),B(x2,y2),
由韦达定理可得x1+x2=-$\frac{2km}{4+{k}^{2}}$,x1x2=$\frac{{m}^{2}-4}{4+{k}^{2}}$,
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=$\frac{4{m}^{2}-4{k}^{2}}{4+{k}^{2}}$,
∵直线与圆O:x2+y2=$\frac{4}{5}$相切,
∴d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{\frac{4}{5}}$,∴5m2=4k2+4,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=$\frac{5{m}^{2}-4-4{k}^{2}}{4+{k}^{2}}$=0,
综上可得OA⊥OB;
(2)解:由(1)知当切线斜率不存在时,|AB|=$\frac{4\sqrt{5}}{5}$;
当切线斜率存在时,由弦长公式可得|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|
=$\sqrt{(1+{k}^{2})[(\frac{-2km}{4+{k}^{2}})^{2}-\frac{4({m}^{2}-4)}{4+{k}^{2}}]}$,
把5m2=4k2+4代入化简可得|AB|=4$\sqrt{\frac{(1+{k}^{2})(16+{k}^{2})}{5(4+{k}^{2})^{2}}}$,
令4+k2=t,则t≥4,且k2=t-4,
代入上式可得|AB|=4$\sqrt{\frac{{t}^{2}+9t-36}{5{t}^{2}}}$=$\frac{4}{\sqrt{5}}$$\sqrt{\frac{25}{16}-36(\frac{1}{t}-\frac{1}{8})^{2}}$,
由t≥4可得0<$\frac{1}{t}$≤$\frac{1}{4}$,当t=8即k=±2时,|AB|取得最大值$\sqrt{5}$;
∴|AB|的取值范围为[$\frac{4\sqrt{5}}{5}$,$\sqrt{5}$].
点评 本题考查直线和圆相切的条件,考查椭圆的性质,涉及直线和圆锥曲线的位置关系以及弦长公式,属于中档题.

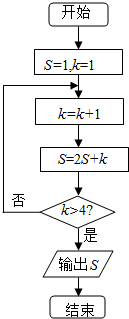 某程序框图如图所示,则输出的结果S等于( )
某程序框图如图所示,则输出的结果S等于( )| A. | 26 | B. | 57 | C. | 60 | D. | 61 |
 在正三棱柱ABC-A1B1C1中,点D是AB的中点,证明:
在正三棱柱ABC-A1B1C1中,点D是AB的中点,证明: