题目内容
18．设全集为R，集合A={x|x2-9x+18≥0}，B={x|y=$\frac{1}{\sqrt{x+2}}$+lg（9-x）．（1）求A∪B，（∁RA）∩B；
（2）已知C={x|a＜x＜a+1}若C⊆B，求实数a的取值范围．
分析 （1）分别求出不等式的解集和函数的定义域出集合A，B，再求出A的补集，再根据并集定义即可求出；
（2）根据C⊆B，得到关于a的不等式组，解得即可．
解答 解：由题意得A={x|x≤3或x≥6}，B={x|-2＜x＜9}
（1）A∪B=R，∁RA={x|3＜x＜6}，
∴（∁RA）∩B={x|3＜x＜6}．
（2）∵C={x|a＜x＜a+1}，且C⊆B，
∴$\left\{\begin{array}{l}{a≥-2}\\{a+1≤9}\end{array}\right.$，
∴所求实数a的取值范围是-2≤a≤8，
点评 本题考查了并集补集及其运算，熟练掌握并集补集的定义是解本题的关键．
练习册系列答案
相关题目
9．命题p：x＞4；命题q：4＜x＜10，则p是q成立的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
10．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | $\frac{1}{3}$+$\frac{π}{12}$ | B． | 1+$\frac{π}{12}$ | C． | $\frac{1}{3}$$+\frac{π}{4}$ | D． | 1$+\frac{π}{4}$ |
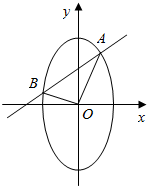已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1，定点N（0，1），过圆M：x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点．