题目内容
2.对任意的x,y∈R函数f(x)都满足f(x+y)=f(x)+f(y)+1恒成立,则f(4)+f(3)+f(2)+f(1)+f(0)+f(-1)+f(-2)+f(-3)+f(-4)=( )| A. | 1 | B. | -9 | C. | -8 | D. | 2 |
分析 f(x+y)=f(x)+f(y)+1,即为f(x+y)+1=[f(x)+1]+[f(y)+1],令g(x)=f(x)+1,判断g(x)为奇函数,即可得到所求值.
解答 解:f(x+y)=f(x)+f(y)+1,即为
f(x+y)+1=[f(x)+1]+[f(y)+1],
令g(x)=f(x)+1,则g(x+y)=g(x)+g(y),
令x=y=0,可得g(0)=0,
令y=-x,可得g(0)=g(x)+g(-x)=0,
即有g(x)为奇函数,
则f(x)+f(-x)=-2,f(0)=-1,
则f(4)+f(3)+f(2)+f(1)
+f(0)+f(-1)+f(-2)+f(-3)+f(-4)=-2×4-1=-9.
故选:B.
点评 本题考查抽象函数的奇偶性的判断和运用:求函数值,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{3}$+$\frac{π}{12}$ | B. | 1+$\frac{π}{12}$ | C. | $\frac{1}{3}$$+\frac{π}{4}$ | D. | 1$+\frac{π}{4}$ |
14.a、b为任意实数,若(a,b)在曲线f(x,y)=0上,且(b,a)也在曲线f(x,y)=0上,则曲线f(x,y)=0的几何特征是( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
12.已知等差数列{an}满足a3=7,a5+a7=26,则通项公式an=( )
| A. | 2n-1 | B. | 2n+1 | C. | 3n+1 | D. | 4n+1 |
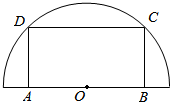 如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.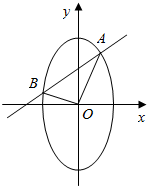 已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1,定点N(0,1),过圆M:x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点.
已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1,定点N(0,1),过圆M:x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点.