题目内容
已知
、
、
为单位向量,若3
+λ
+7
=
,且
、
夹角为
,则λ= .
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| 2π |
| 3 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:首先,根据3
+λ
+7
=
,得到7
=-(3
+λ
),然后,两边平方,得49|
|2=9|
|2+6λ|
||
|cos
+λ2|
|2,然后,结合
、
、
为单位向量,建立等式求解λ的值即可.
| a |
| b |
| c |
| 0 |
| c |
| a |
| b |
| c |
| a |
| a |
| b |
| 2π |
| 3 |
| b |
| a |
| b |
| c |
解答:
解:∵3
+λ
+7
=
,
∴7
=-(3
+λ
),
两边平方,得
49|
|2=9|
|2+6λ|
||
|cos
+λ2|
|2,
∵
、
、
为单位向量,
∴49=9-3λ+λ2,
∴λ=-5或8.
故答案为:-5或8.
| a |
| b |
| c |
| 0 |
∴7
| c |
| a |
| b |
两边平方,得
49|
| c |
| a |
| a |
| b |
| 2π |
| 3 |
| b |
∵
| a |
| b |
| c |
∴49=9-3λ+λ2,
∴λ=-5或8.
故答案为:-5或8.
点评:本题重点考查了数量积的性质、单位向量的概念和性质运用等知识属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设点O是△ABC的外心,AB=13,AC=12,则
•
为( )
| BC |
| AO |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如果
<θ<
,那么下列各式中正确的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosθ<tanθ<sinθ |
| B、sinθ<cosθ<tanθ |
| C、tanθ<sinθ<cosθ |
| D、cosθ<sinθ<tanθ |
已知θ是三角形的一个内角,且sinθ+cosθ=
,则x2sinθ-y2cosθ=1表示( )
| 1 |
| 2 |
| A、焦点在x轴上的椭圆 |
| B、焦点在x轴上的双曲线 |
| C、焦点在y轴上的椭圆 |
| D、焦点在y轴上的双曲线 |
如图所示的程序输出的结果S为( )


| A、17 | B、19 | C、21 | D、23 |
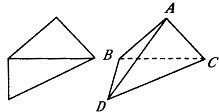 如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述中正确的是.
如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述中正确的是.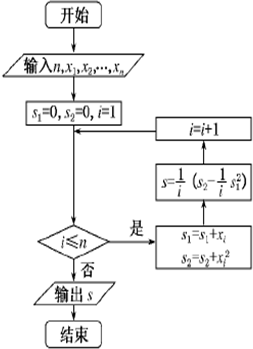 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为