题目内容
（2012•包头一模）函数f（x）=sin（ωx+?）（其中|?|＜| π |
| 2 |
分析：根据周期求出ω，再由五点法作图求出∅，从而得到函数f（x）=sin2（x+
），故把y=f（x）的图象向右平移
个单位长度可得y=sinωx的图象，从而得出结论．
| π |
| 6 |
| π |
| 6 |
解答：解：由题意可得
×
=
-
=
，∴ω=2．
再由五点法作图可得 2×
+∅=π，∴∅=
，故函数f（x）=sin（ωx+?）=sin（2x+
）=sin2（x+
）．
故把y=f（x）的图象向右平移
个单位长度可得y=sinωx的图象，
故选A．
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
| π |
| 4 |
再由五点法作图可得 2×
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
故把y=f（x）的图象向右平移
| π |
| 6 |
故选A．
点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求函数的解析式，函数y=Asin（ωx+∅）的图象变换，属于中档题．
练习册系列答案
相关题目
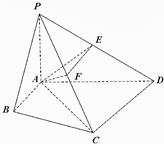（2012•包头一模）在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2，AB=1．