题目内容
12.计算$\int_{\frac{π}{2}}^π{sinx}$dx=1.分析 根据定积分的计算法则计算即可.
解答 解:$\int_{\frac{π}{2}}^π{sinx}$dx=-cosx|${\;}_{\frac{π}{2}}^{π}$=-(cosπ-cos$\frac{π}{2}$)=1;
故答案为:1.
点评 本题考查了定积分的计算,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
7.阅读程序框图,任意输入一次x(-1≤x≤1)与y(-1≤y≤1),则能输出数对(x,y)的概率为( )
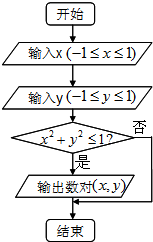

| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
1.给出的下列函数中在$(\frac{π}{2},π)$上是增函数的是( )
| A. | y=sinx | B. | y=cosx | C. | y=sin2x | D. | y=cos2x |