Question

选修4－1：平面几何证明选讲

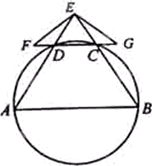
如图，AB是⊙O的直径，点P在AB的延长线上，PC与⊙O相切于点C，PC＝AC＝1．求⊙O的半径．

Answer 1

答案：
解析：

解：连接OC． 　　设∠PAC＝．因为PC＝AC，所以∠CPA＝，∠COP＝2． 　　又因为PC与⊙O相切于点C，所以OC⊥PC． 　　所以3＝90°，所以＝30°． 　　设⊙O的半径为r，在Rt△POC中， 　　r＝CP·tan30°＝1×＝．