题目内容
求证:若三角形的三内角 对应的边分别为
对应的边分别为 ,且
,且 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则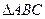 是正三角形。并分析在证明过程中用了几次三段论,分别写出每次三段论的大前提、小前提与结论。
是正三角形。并分析在证明过程中用了几次三段论,分别写出每次三段论的大前提、小前提与结论。
 对应的边分别为
对应的边分别为 ,且
,且 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则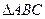 是正三角形。并分析在证明过程中用了几次三段论,分别写出每次三段论的大前提、小前提与结论。
是正三角形。并分析在证明过程中用了几次三段论,分别写出每次三段论的大前提、小前提与结论。证明见解析
证明:由 成等差数列,得
成等差数列,得 ,
,
又 ,所以
,所以
由 成等比数列,得
成等比数列,得
那么 ,即
,即 ,得
,得
由于,有一个角是60 的等腰三角形是等边三角形
的等腰三角形是等边三角形
故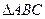 是正三角形
是正三角形
上述证明过程共四次使用了三段论。
第一次,大前提“若 成等差数列,则
成等差数列,则 ”;小前提“三角形三内角
”;小前提“三角形三内角 成等差数列,
成等差数列, ”;结论“
”;结论“ ,所以
,所以 ”。
”。
第二次,大前提“若 成等比数列,则
成等比数列,则 ”;小前提“三角形的三边
”;小前提“三角形的三边 成等比数列”;结论“
成等比数列”;结论“ ”。
”。
第三次,大前提“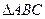 中,
中, ”;小前提“
”;小前提“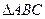 中,
中, ”;结论“
”;结论“
 ,即
,即 ,所以
,所以 ”。
”。
第四次,大前提“有一个角是60 的等腰三角形是等边三角形”;小前提“
的等腰三角形是等边三角形”;小前提“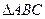 中,
中, ,
, ”;结论“
”;结论“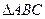 是一个等边三角形”。
是一个等边三角形”。
 成等差数列,得
成等差数列,得 ,
,又
 ,所以
,所以
由
 成等比数列,得
成等比数列,得
那么
 ,即
,即 ,得
,得
由于,有一个角是60
 的等腰三角形是等边三角形
的等腰三角形是等边三角形故
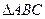 是正三角形
是正三角形上述证明过程共四次使用了三段论。
第一次,大前提“若
 成等差数列,则
成等差数列,则 ”;小前提“三角形三内角
”;小前提“三角形三内角 成等差数列,
成等差数列, ”;结论“
”;结论“ ,所以
,所以 ”。
”。第二次,大前提“若
 成等比数列,则
成等比数列,则 ”;小前提“三角形的三边
”;小前提“三角形的三边 成等比数列”;结论“
成等比数列”;结论“ ”。
”。第三次,大前提“
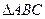 中,
中, ”;小前提“
”;小前提“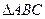 中,
中, ”;结论“
”;结论“
 ,即
,即 ,所以
,所以 ”。
”。第四次,大前提“有一个角是60
 的等腰三角形是等边三角形”;小前提“
的等腰三角形是等边三角形”;小前提“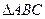 中,
中, ,
, ”;结论“
”;结论“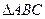 是一个等边三角形”。
是一个等边三角形”。
练习册系列答案
相关题目
 ,把这个结论推广到空间正四面体,类似的结论是______.
,把这个结论推广到空间正四面体,类似的结论是______. (c≠0)”
(c≠0)” 得其中
得其中 的值依次是____________.
的值依次是____________. 中,
中, ,若
,若 ,则
,则 ;若类比该命题,如图(2),三棱锥
;若类比该命题,如图(2),三棱锥 中,
中, 面
面 点在三角形
点在三角形 所在平面内的射影为
所在平面内的射影为 ,则有什么结论?命题是否是真命题.
,则有什么结论?命题是否是真命题.
 且
且 ,求
,求 的值.(先观察
的值.(先观察 时的值,归纳猜测
时的值,归纳猜测 内( )
内( ) ,结论是:
,结论是: ,那么这个演绎推理所得结论错误的原因是:( ﹡ ).
,那么这个演绎推理所得结论错误的原因是:( ﹡ ). ,其中
,其中 为常数,等号右边的运算是通常意义的加乘运算,现已知
为常数,等号右边的运算是通常意义的加乘运算,现已知 ,
, ,且有一个非零实数m,使得对任意实数x,都有
,且有一个非零实数m,使得对任意实数x,都有 ,则
,则 ______________。
______________。