题目内容
已知函数f(n)= 其中n∈N,则f(8)等于
其中n∈N,则f(8)等于
- A.2
- B.4
- C.6
- D.7
D
分析:根据解析式先求出f(8)=f[f(13)],依次再求出f(13)和f[f(13)],即得到所求的函数值.
解答:∵函数f(n)= ,
,
∴f(8)=f[f(13)],
则f(13)=13-3=10,
∴f(8)=f[f(13)]=10-3=7,
答案为:7.
故选D.
点评:本题是函数求值问题,对应多层求值按“由里到外”的顺序逐层求值,一定要注意自变量的值所在的范围,然后代入相应的解析式求解.
分析:根据解析式先求出f(8)=f[f(13)],依次再求出f(13)和f[f(13)],即得到所求的函数值.
解答:∵函数f(n)=
 ,
,∴f(8)=f[f(13)],
则f(13)=13-3=10,
∴f(8)=f[f(13)]=10-3=7,
答案为:7.
故选D.
点评:本题是函数求值问题,对应多层求值按“由里到外”的顺序逐层求值,一定要注意自变量的值所在的范围,然后代入相应的解析式求解.

练习册系列答案
相关题目
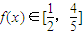 时,求x的取值范围;
时,求x的取值范围; 恒成立,求最小的N;
恒成立,求最小的N; .
.