题目内容
已知函数f(x)在其定义域上满足xf(x)+2af(x)=x+a-1(a>0).(1)函数y=f(x)的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
(2)当
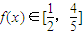 时,求x的取值范围;
时,求x的取值范围;(3)若f(0)=0,数列{an}满足a1=1,那么:
①若0<an+1≤f(an),正整数N满足n>N时,对所有适合上述条件的数列{an},
 恒成立,求最小的N;
恒成立,求最小的N;②若an+1=f(an),求证:
 .
.
【答案】分析:(1)依题意有(x+2a)f(x)=x+a-1.若x=-2a,得a=-1,这与a>0矛盾,故x≠-2a,所以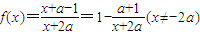 ,由此知y=f(x)的图象是中心对称图形,并能求出其对称中心.
,由此知y=f(x)的图象是中心对称图形,并能求出其对称中心.
(2)由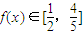 ,知
,知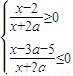 ,由a>0,能求出x的取值范围.
,由a>0,能求出x的取值范围.
(3)①由f(0)=0得a=1,故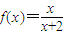 .由
.由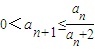 ,得
,得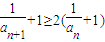 .令
.令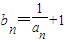 ,则bn+1≥2bn,由此能求推导出满足题设要求的最小正整数.
,则bn+1≥2bn,由此能求推导出满足题设要求的最小正整数.
②由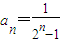 ,知
,知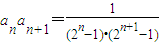 ,
,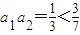 ,
,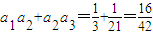
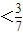 ,故当n=1,2时,不等式成立.当n≥2时,由
,故当n=1,2时,不等式成立.当n≥2时,由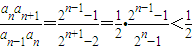 ,能够证明
,能够证明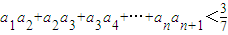 .
.
解答:解:(1)依题意有(x+2a)f(x)=x+a-1.
若x=-2a,则x+a-1=-a-1=0,得a=-1,这与a>0矛盾,
∴x≠-2a,
∴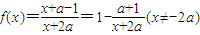 ,
,
故y=f(x)的图象是中心对称图形,其对称中心为点(-2a,1).
(2)∵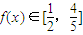 ,
,
∴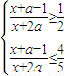 即
即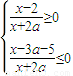
又∵a>0,∴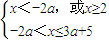
得x∈[2,3a+5].
(3)①由f(0)=0得a=1,
∴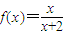 .
.
由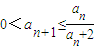 得
得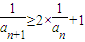 ,
,
即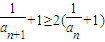 .
.
令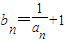 ,则bn+1≥2bn,
,则bn+1≥2bn,
又∵an>0,∴bn>0,∴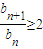 .
.
∵a1=1,∴b1=2,
∴当n≥2时,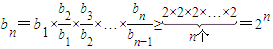 .
.
又∵b1=2也符合bn≥2n,
∴bn≥2n(n∈N*),即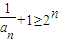 ,
,
得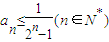 .
.
要使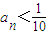 恒成立,
恒成立,
只需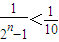 ,即2n>11,
,即2n>11,
∴n>3.故满足题设要求的最小正整数N=3.
②由①知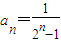 ,
,
∴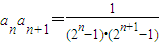 ,
,
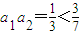 ,
,
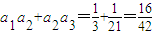
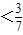 ,
,
∴当n=1,2时,不等式成立.
当n≥2时,
∵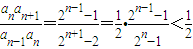 ,
,
∴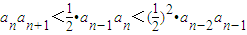
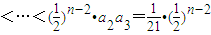 ,
,
∴
=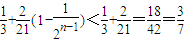 .
.
点评:本题考查数列和不等式的综合应用,考查数列的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对计算能力的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.
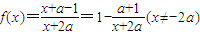 ,由此知y=f(x)的图象是中心对称图形,并能求出其对称中心.
,由此知y=f(x)的图象是中心对称图形,并能求出其对称中心.(2)由
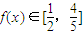 ,知
,知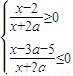 ,由a>0,能求出x的取值范围.
,由a>0,能求出x的取值范围.(3)①由f(0)=0得a=1,故
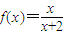 .由
.由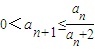 ,得
,得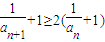 .令
.令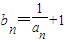 ,则bn+1≥2bn,由此能求推导出满足题设要求的最小正整数.
,则bn+1≥2bn,由此能求推导出满足题设要求的最小正整数.②由
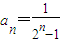 ,知
,知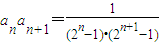 ,
,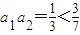 ,
,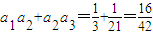
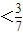 ,故当n=1,2时,不等式成立.当n≥2时,由
,故当n=1,2时,不等式成立.当n≥2时,由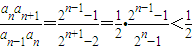 ,能够证明
,能够证明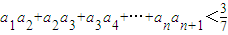 .
.解答:解:(1)依题意有(x+2a)f(x)=x+a-1.
若x=-2a,则x+a-1=-a-1=0,得a=-1,这与a>0矛盾,
∴x≠-2a,
∴
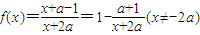 ,
,故y=f(x)的图象是中心对称图形,其对称中心为点(-2a,1).
(2)∵
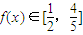 ,
,∴
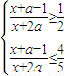 即
即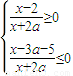
又∵a>0,∴
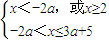
得x∈[2,3a+5].
(3)①由f(0)=0得a=1,
∴
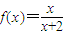 .
.由
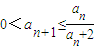 得
得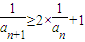 ,
,即
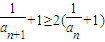 .
.令
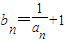 ,则bn+1≥2bn,
,则bn+1≥2bn,又∵an>0,∴bn>0,∴
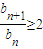 .
.∵a1=1,∴b1=2,
∴当n≥2时,
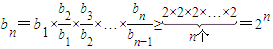 .
.又∵b1=2也符合bn≥2n,
∴bn≥2n(n∈N*),即
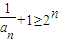 ,
,得
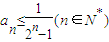 .
.要使
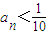 恒成立,
恒成立,只需
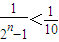 ,即2n>11,
,即2n>11,∴n>3.故满足题设要求的最小正整数N=3.
②由①知
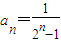 ,
,∴
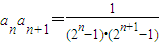 ,
,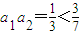 ,
,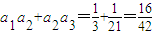
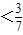 ,
,∴当n=1,2时,不等式成立.
当n≥2时,
∵
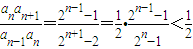 ,
,∴
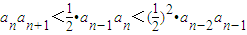
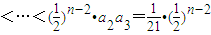 ,
,∴

=
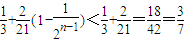 .
.点评:本题考查数列和不等式的综合应用,考查数列的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对计算能力的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
 在M内为增函数.
在M内为增函数.