题目内容
已知 ,记数列{an}的前n项和为Sn,则使Sn>0的n的最小值为
,记数列{an}的前n项和为Sn,则使Sn>0的n的最小值为
- A.10
- B.11
- C.12
- D.13
B
分析:由 ,可得a1+a10=a2+a9=…=a5+a6=0,a11>0,则有S9<0,S10=0,S11>0可求
,可得a1+a10=a2+a9=…=a5+a6=0,a11>0,则有S9<0,S10=0,S11>0可求
解答:由 ,
,
可得a1+a10=a2+a9=…=a5+a6=0,a11>0
∴S9<0,S10=0,S11>0
使Sn>0的n的最小值为11
故选:B
点评:本题主要考查了由数列的递推公式求解数列的和,解题的关键是归纳出a1+a10=a2+a9=…=a5+a6=0,a11>0
分析:由
 ,可得a1+a10=a2+a9=…=a5+a6=0,a11>0,则有S9<0,S10=0,S11>0可求
,可得a1+a10=a2+a9=…=a5+a6=0,a11>0,则有S9<0,S10=0,S11>0可求解答:由
 ,
,可得a1+a10=a2+a9=…=a5+a6=0,a11>0
∴S9<0,S10=0,S11>0
使Sn>0的n的最小值为11
故选:B
点评:本题主要考查了由数列的递推公式求解数列的和,解题的关键是归纳出a1+a10=a2+a9=…=a5+a6=0,a11>0

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
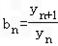 .
.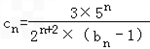 ,数列{cn}的前n项和为Tn,
,数列{cn}的前n项和为Tn, ;
;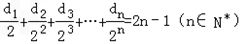 ,记数列{an}的前n项和为An,数列{dn}的前n项和为Bn,试比较An与
,记数列{an}的前n项和为An,数列{dn}的前n项和为Bn,试比较An与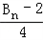 的大小.
的大小.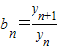 .
.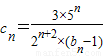 ,数列{cn}的前n项和为Tn,求证:
,数列{cn}的前n项和为Tn,求证: ;
;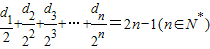 ,记数列{an}的前n项和为An,数列{dn}的前n项和为Bn,试比较An与
,记数列{an}的前n项和为An,数列{dn}的前n项和为Bn,试比较An与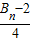 的大小.
的大小.