题目内容
(本小题14分)
已知函数y=x2-2ax+1(a为常数)在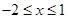 上的最小值为
上的最小值为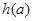 ,试将
,试将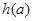 用a表示出来,并求出
用a表示出来,并求出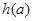 的最大值.
的最大值.
已知函数y=x2-2ax+1(a为常数)在
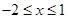 上的最小值为
上的最小值为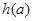 ,试将
,试将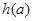 用a表示出来,并求出
用a表示出来,并求出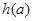 的最大值.
的最大值.
 .
. 解决二次函数的最值问题,应该先求出二次函数的对称轴,判断出对称轴与区间的关系,进一步判断出二次函数的单调性,进一步求出函数的最值.由该函数的性质可知,该函数的最小值与抛物线的对称轴的位置有关,于是需要对对称轴的位置进行分类讨论.
解:∵y=(x-a)2+1-a2, ∴抛物线y=x2-2ax+1的对称轴方程是 .
.
(1)当 时,由图①可知,当
时,由图①可知,当 时,该函数取最小值
时,该函数取最小值 ;
;
(2) 当 时, 由图②可知, 当
时, 由图②可知, 当 时,该函数取最小值
时,该函数取最小值  ;
;
(3) 当a>1时, 由图③可知, 当 时,该函数取最小值
时,该函数取最小值
综上,函数的最小值为
 ………………8分
………………8分
 (1)当
(1)当 时,
时,
⑵当 时,
时,
⑶当a>1时, ,
,
综上所述, . ………………14分
. ………………14分
解:∵y=(x-a)2+1-a2, ∴抛物线y=x2-2ax+1的对称轴方程是
 .
.(1)当
 时,由图①可知,当
时,由图①可知,当 时,该函数取最小值
时,该函数取最小值 ;
;(2) 当
 时, 由图②可知, 当
时, 由图②可知, 当 时,该函数取最小值
时,该函数取最小值  ;
;(3) 当a>1时, 由图③可知, 当
 时,该函数取最小值
时,该函数取最小值
综上,函数的最小值为
 ………………8分
………………8分 (1)当
(1)当 时,
时,
⑵当
 时,
时,
⑶当a>1时,
 ,
, 综上所述,
 . ………………14分
. ………………14分
练习册系列答案
相关题目
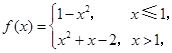 则
则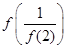 的值为( )
的值为( )




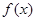 的图像简图,并指出函数
的图像简图,并指出函数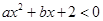 的解集为
的解集为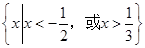 ,则
,则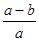 的值为( )
的值为( )

 的值域是
的值域是 ,则
,则 的最小值是 .
的最小值是 .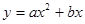 与
与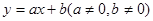 的函数图象只可能是( )
的函数图象只可能是( )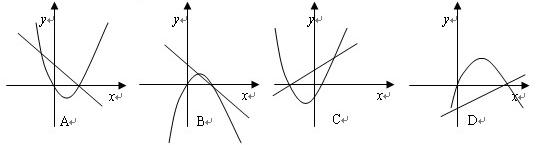
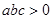 ,二次函数
,二次函数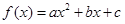 的图像可能是
的图像可能是 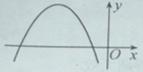
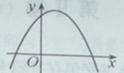
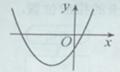
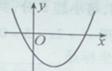
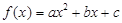 .
.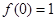 ,
,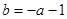 ,解关于x不等式
,解关于x不等式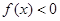 ;
;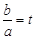 ,请把
,请把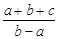 表示成关于t的函数g(t),并求g(t)的最小值.
表示成关于t的函数g(t),并求g(t)的最小值.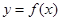 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为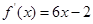 ,数列
,数列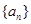 的前n项和为
的前n项和为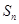 ,点
,点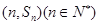 均在函数
均在函数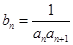 ,
,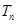 是数列
是数列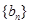 的前n项和,求使得
的前n项和,求使得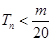 对所有
对所有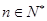 都成立的最小正整数m;
都成立的最小正整数m;