题目内容

已知-

π

2

＜θ＜

π

2

，且sinθ+cosθ=a，其中a∈（0，1），则关于tanθ的值，在以下四个答案中，可能正确的是（　　）

A．-3

B．3或

1

3

C．-

1

3

D．-3或-

1

3

由-

π

2

＜θ＜

π

2

，得到cosθ＞0，
所以把sinθ+cosθ=a两边平方得：
（sinθ+cosθ）²=a²，
即sin²θ+cos²θ+2sinθcosθ=1+2sinθcosθ=a²，又a∈（0，1），
所以2sinθcosθ=a²-1＜0，所以sinθ＜0，
又sinθ+cosθ=a＞0，
所以cosθ＞-sinθ＞0，
则-1＜tanθ＜0．
故选C

练习册系列答案

小学课时作业全通练案系列答案

一天一练系列答案

一线调研今年新试卷系列答案

金版课堂课时训练系列答案

单元全能练考卷系列答案

小学同步全程测试卷一考通系列答案

新黄冈兵法密卷系列答案

特优练考卷系列答案

一通百通顶尖单元练系列答案

快乐AB卷系列答案

相关题目

已知如图是函数y=2sin（ωx+φ）（|φ|＜

）的图象，那么（　　）

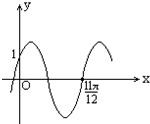
，π)，且sin（π-α)+cos(2π+α)=

+cos（2π+α）=

求证：（1）sinα-cosα；
（2）tanα；
（3）sin³(

已知函数f（x）的定义域为R，则下列命题中：?
①若f（x-2）是偶函数，则函数f（x）的图象关于直线x=2对称；?②若f（x+2）=-f（x-2），则函数f（x）的图象关于原点对称；?③函数y=f（2+x）与函数y=f（2-x）的图象关于直线x=2对称；?④函数y=f（x-2）与函数y=f（2-x）的图象关于直线x=2对称．?
其中正确的命题序号是

已知函数f（x）=ln（x-1）-k（x-1）+1（k∈R）．
（1）若k=2，求以M（2，f（2））为切点的曲线的切线方程；
（2）若函数f（x）≤0恒成立，确定实数K的取值范围；
（3）证明：

已知函数f（x）的定义域为R，则下列命题中：?
①若f（x-2）是偶函数，则函数f（x）的图象关于直线x=2对称；?②若f（x+2）=-f（x-2），则函数f（x）的图象关于原点对称；?③函数y=f（2+x）与函数y=f（2-x）的图象关于直线x=2对称；?④函数y=f（x-2）与函数y=f（2-x）的图象关于直线x=2对称．?
其中正确的命题序号是________．?