题目内容
已知函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数f(x)在 的最大值.
的最大值.
解:(Ⅰ)∵f(x)= -sin2x,
-sin2x,
∴f( )=
)= -
- =cos
=cos =
= .…(5分)
.…(5分)
(Ⅱ)∵f(x)= -sin2x
-sin2x
= [1+cos(2x-
[1+cos(2x- )]-
)]- (1-cos2x)
(1-cos2x)
= [cos(2x-
[cos(2x- )+cos2x]
)+cos2x]
= (
( sin2x+
sin2x+ cos2x)
cos2x)
= sin(2x+
sin(2x+ ),.…(9分)
),.…(9分)
∵x∈[0, ],
],
∴2x+ ∈[
∈[ ,
, ],
],
∴当2x+ =
= ,即x=
,即x= 时,f(x)取得最大值
时,f(x)取得最大值 .…(12分)
.…(12分)
分析:(Ⅰ)将x= 代入已知关系式即可求得其值;
代入已知关系式即可求得其值;
(Ⅱ)由x∈[0, ],可求得2x+
],可求得2x+ ∈[
∈[ ,
, ],利用正弦函数的性质即可求得f(x)的最大值.
],利用正弦函数的性质即可求得f(x)的最大值.
点评:本题考查三角函数中的恒等变换应用,考查复合三角函数的单调性,求得f(x)的解析式是关键,也是难点,属于中档题.
 -sin2x,
-sin2x,∴f(
 )=
)= -
- =cos
=cos =
= .…(5分)
.…(5分)(Ⅱ)∵f(x)=
 -sin2x
-sin2x=
 [1+cos(2x-
[1+cos(2x- )]-
)]- (1-cos2x)
(1-cos2x)=
 [cos(2x-
[cos(2x- )+cos2x]
)+cos2x]=
 (
( sin2x+
sin2x+ cos2x)
cos2x)=
 sin(2x+
sin(2x+ ),.…(9分)
),.…(9分)∵x∈[0,
 ],
],∴2x+
 ∈[
∈[ ,
, ],
],∴当2x+
 =
= ,即x=
,即x= 时,f(x)取得最大值
时,f(x)取得最大值 .…(12分)
.…(12分)分析:(Ⅰ)将x=
 代入已知关系式即可求得其值;
代入已知关系式即可求得其值;(Ⅱ)由x∈[0,
 ],可求得2x+
],可求得2x+ ∈[
∈[ ,
, ],利用正弦函数的性质即可求得f(x)的最大值.
],利用正弦函数的性质即可求得f(x)的最大值.点评:本题考查三角函数中的恒等变换应用,考查复合三角函数的单调性,求得f(x)的解析式是关键,也是难点,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
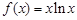 .
.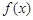 的最小值;
的最小值;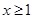 都有
都有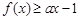 ,求实数
,求实数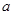 的取值范围.
的取值范围.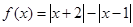
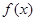 的值域;
的值域;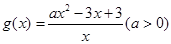 ,若对
,若对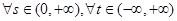 恒有
恒有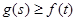 成立,试求实数
成立,试求实数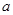 的取值氛围。
的取值氛围。 ,(1)求
,(1)求 的定义域;
的定义域; 是第四象限的角,且
是第四象限的角,且 ,求
,求 的值。
的值。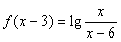 ,
,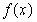 的解析式;
的解析式; .
.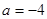 时,求
时,求 的最小值;
的最小值;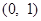 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;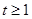 时,不等式
时,不等式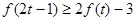 恒成立,求实数
恒成立,求实数