题目内容
【题目】设函数![]() .
.
(1)求函数的单调区间;
(2)若![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(3)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的值.
的值.
【答案】(1)![]() 的单调递减区间
的单调递减区间![]() ,单调递增区间是
,单调递增区间是![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析: ![]() 求导,令
求导,令![]() ,求出极值点,得到单调区间
,求出极值点,得到单调区间
![]() 由
由![]() 得到最小值,代入到
得到最小值,代入到![]() ,求出结果
,求出结果
![]() 令
令![]() ,求导算出最大值,再令
,求导算出最大值,再令![]() ,化简为
,化简为![]() ,结合
,结合![]() 和单调性求出结果;
和单调性求出结果;
解析:(1)![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() ,
, ![]() ;当
;当![]() ,
, ![]() ,
,
故函数![]() 的单调递减区间
的单调递减区间![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)由(1)知当![]() 时
时![]() 取得最小值;
取得最小值;
从而![]() 等价于
等价于![]() ;
;
又![]()
![]() ;即
;即![]() ,
,
等价于![]() ;又因为
;又因为![]() (求导易证
(求导易证![]() 取等),
取等),
故![]() ,故只有
,故只有![]() ,即
,即![]() ;
;
(3)令![]() ,
, ![]() ,从而当
,从而当![]() 时,
时, 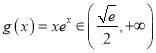 ,
,
![]() ,令
,令![]() ,即
,即![]() ;原问题转化为:
;原问题转化为:
当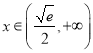 时,
时, ![]() 恒成立;
恒成立;
若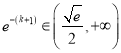 ,由(1)知必有
,由(1)知必有![]() ,由(2)知:
,由(2)知: ![]() ,
,
若 ,即
,即![]() ,则由(1)知
,则由(1)知![]() 在区间
在区间 上单调递增,又
上单调递增,又![]() ,所以
,所以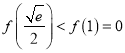 ,不合题意;
,不合题意;
综上, ![]() .
.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
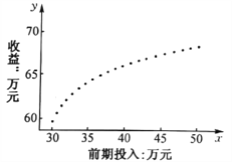
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近期前期广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共
(单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共![]() 个数据点)及一些统计量的值.为了进一步了解广告投入量
个数据点)及一些统计量的值.为了进一步了解广告投入量![]() 对收益
对收益![]() 的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
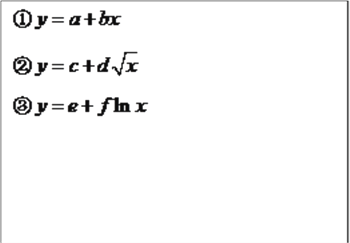
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据![]() ,
, ![]() ,参考数据:
,参考数据: ![]() ,
, ![]() .
.
(1)根据散点图判断,哪一位员工提出的模型不适合用来描述![]() 与
与![]() 之间的关系?简要说明理由.
之间的关系?简要说明理由.
(2)根据(1)的判断结果及表中数据,在余下两个模型中分别建立收益![]() 关于投入量
关于投入量![]() 的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益
的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益![]() 的回归方程)?说明理由;
的回归方程)?说明理由;
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率、截距的最小二乘估计以及相关系数分别为:
的斜率、截距的最小二乘估计以及相关系数分别为:
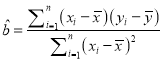 ,
, ![]() ,
, 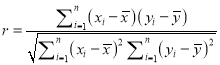 ,
,
其中![]() 越接近于
越接近于![]() ,说明变量
,说明变量![]() 与
与![]() 的线性相关程度越好.
的线性相关程度越好.
