题目内容
(本小题12分) 定义:若函数f(x)对于其定义域内的某一数x0,有f(x0)= x0,则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ 对称,求b的最小值.
对称,求b的最小值.
(1)-1或3;(2)0<a<1;(3)bmin=-1
【解析】(1)f(x)=x2-x-3,由x2-x-3=x,解得 x=3或-1,
所以所求的不动点为-1或3. ………………………3分
(2)令ax2+(b+1)x+b-1=x,则ax2+bx+b-1=0 ①
由题意,方程①恒有两个不等实根,所以△=b2-4a(b-1)>0,
即b2-4ab+4a>0恒成立,………………………………5分
则△¢=16a2-16a<0,故0<a<1 …………………………7分[来源:学+科+网Z+X+X+K]
(3)设A(x1,x1),B(x2,x2)(x1≠x2),则kAB=1,∴k=﹣1,
所以y=-x+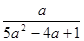 ,
……………………………………8分
,
……………………………………8分
又AB的中点在该直线上,所以=﹣+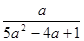 ,
,
∴x1+x2=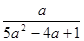 ,
,
而x1、x2应是方程①的两个根,所以x1+x2=﹣,即﹣=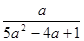 ,
,
∴b=﹣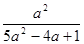 …………………………………………10分
…………………………………………10分
=-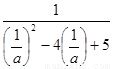 =-
=-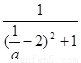
∴当 a=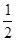 ∈(0,1)时,bmin=-1
.………………………………12分
∈(0,1)时,bmin=-1
.………………………………12分

 (Ⅲ)如果点A的坐标为
(Ⅲ)如果点A的坐标为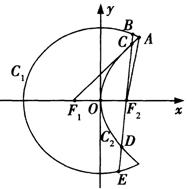

 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 是曲线
是曲线 为钝角,若
为钝角,若 ,
, .
. 、
、 、
、 、
、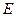 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由. 的取值范围.(其中O为坐标原点)
的取值范围.(其中O为坐标原点)