题目内容
(本小题12分)
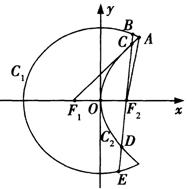
如图,曲线![]() 是以原点
是以原点![]() 为中心,以
为中心,以![]() 、
、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以
是以![]() 为顶点,以
为顶点,以![]() 为焦点的抛物线的一部分,
为焦点的抛物线的一部分,![]() 是曲线
是曲线![]() 和
和![]() 的交点,且
的交点,且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.
(I)求曲线![]() 和
和![]() 所在的椭圆和抛物线的方程;
所在的椭圆和抛物线的方程;
(II)过![]() 作一条与轴不垂直的直线,分别与曲线
作一条与轴不垂直的直线,分别与曲线![]() 、
、![]() 依次交于
依次交于![]() 、
、![]() 、
、![]() 、
、![]() 四点(如图),若
四点(如图),若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,问
的中点,问![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
(1)椭圆的方程为![]() ,抛物线的方程为
,抛物线的方程为![]() (2)是定值3
(2)是定值3
解析:
(I)设椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() ,即抛物线准线,作
,即抛物线准线,作![]() 垂直于该准线,作
垂直于该准线,作![]() 轴于点
轴于点![]() ,则由抛物线的定义得
,则由抛物线的定义得![]()
所以![]()
![]()
![]()
所以![]() ,
,![]() ,
,![]()
由![]() ,得
,得![]() ,
,![]()
所以椭圆的方程为![]() ,抛物线的方程为
,抛物线的方程为![]() . 5分
. 5分
(II)设![]() ,
,![]() ,
,![]() ,
,![]()
由已知得直线![]() 的斜率一定存在,故可设直线的方程为
的斜率一定存在,故可设直线的方程为![]()
由 ,得
,得![]()
得![]() ,
,![]() 7分
7分
同理,由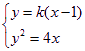 ,得
,得![]()
得![]() ,
,![]() 9分
9分
所以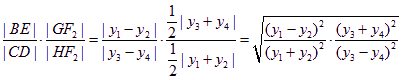
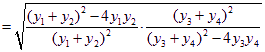
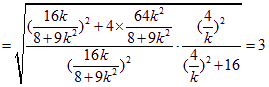 ,为定值. 12分
,为定值. 12分

练习册系列答案
相关题目

 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 是曲线
是曲线 为钝角,若
为钝角,若 ,
, .
. 、
、 、
、 、
、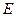 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由. <
< <
< <…<
<…< )是曲线C
)是曲线C
 上的n个点,点
上的n个点,点 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿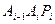 是正三角形(
是正三角形( 是坐标原点)。
是坐标原点)。

 的横坐标
的横坐标 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明 中,
中,
 ,
, 为
为 中点,若规定主视方向为垂直于平面
中点,若规定主视方向为垂直于平面 的方向,则可求得三棱柱左视图的面积为
的方向,则可求得三棱柱左视图的面积为 ;
;
 ;
; 的体积。
的体积。 海里的两个观测点。现位于B点正北方向、A点北偏东
海里的两个观测点。现位于B点正北方向、A点北偏东 方向的C点有一艘轮船发出求救信号,位于B点北偏西
方向的C点有一艘轮船发出求救信号,位于B点北偏西 、A点北偏西
、A点北偏西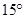 的D点的救援船立即前往营救,其航行速度为
的D点的救援船立即前往营救,其航行速度为 海里/小时.问该救援船到达C点需要多少时间?
海里/小时.问该救援船到达C点需要多少时间?
 的算法的
的算法的