题目内容
已知下列各组命题,其中p是q的充分必要条件的是________.
①p:m≤-2或m≥6;q:y=x2+mx+m+3有两个不同的零点
②p: =1;q:y=f(x)是偶函数
=1;q:y=f(x)是偶函数
③p:cos α=cos β;q:tan α=tan β
④p:A∩B=A;q:A⊆U,B⊆U,∁UB⊆∁UA
④
解析 对于①,由y=x2+mx+m+3有两个不同的零点,可得Δ=m2-4(m+3)>0,从而可得m<-2或m>6.所以p是q的必要不充分条件;
对于②,由 =1⇒f(-x)=f(x)⇒y=f(x)是偶函数,但由y=f(x)是偶函数不能推出
=1⇒f(-x)=f(x)⇒y=f(x)是偶函数,但由y=f(x)是偶函数不能推出 =1,例如函数f(x)=0,所以p是q的充分不必要条件;
=1,例如函数f(x)=0,所以p是q的充分不必要条件;
对于③,当cos α=cos β=0时,不存在tan α=tan β,反之也不成立,所以p是q的既不充分也不必要条件;
对于④,由A∩B=A,知A⊆B,所以∁UB⊆∁UA;
反之,由∁UB⊆∁UA,知A⊆B,即A∩B=A.
所以p⇔q.
综上所述,p是q的充分必要条件的是④.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
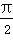 ,π),sin α=
,π),sin α=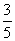 ,则tan(α+
,则tan(α+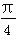 )等于( )
)等于( )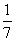 B.7 C.-
B.7 C.-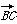 =a,
=a,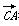 =b且a,b满足:a·b=-9,|a|=3,|b|=5,θ为a,b的夹角.
=b且a,b满足:a·b=-9,|a|=3,|b|=5,θ为a,b的夹角.
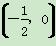 D.
D.