题目内容
已知数列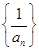 是公差为
是公差为 的等差数列,且
的等差数列,且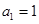 .
.
(1)求数列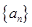 的通项公式;
的通项公式;
(2)设数列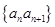 的前
的前 项和为
项和为 .
.
证明: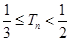 .
.
(1)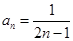 ;(2)证明见解析.
;(2)证明见解析.
解析试题分析:(1)根据题意,要求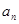 ,首先求
,首先求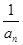 ,因为数列
,因为数列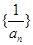 是等差数列,且首项为1,公差为2,由等差数列的通项公式可立即得到
是等差数列,且首项为1,公差为2,由等差数列的通项公式可立即得到 ,从而得
,从而得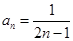 ;(2)要证明相应的不等式,应该先求数列
;(2)要证明相应的不等式,应该先求数列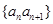 的前
的前 项和,为此要明确这个数列是什么数列,从(1)知数列
项和,为此要明确这个数列是什么数列,从(1)知数列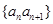 是一个等差数列相邻项相乘取倒数所得,因此其前
是一个等差数列相邻项相乘取倒数所得,因此其前 项和宜采用裂项相消的方法求得,具体就是
项和宜采用裂项相消的方法求得,具体就是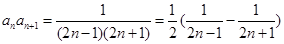 ,这样在和式
,这样在和式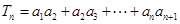 中,前后项可相消为零,从而
中,前后项可相消为零,从而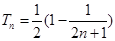 ,从而可知数列
,从而可知数列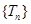 是递增数列,最小项为
是递增数列,最小项为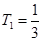 ,又从
,又从 表达式可知
表达式可知 ,不等式得证.
,不等式得证.
试题解析:(1)由已知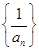 是公差为
是公差为 的等差数列,
的等差数列, 
 ,又
,又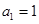 ,
,
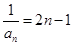 3分
3分
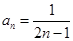 5分
5分
(2)
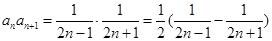 7分
7分
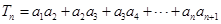
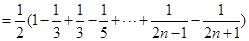
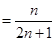 9分
9分
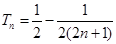 ,
, 随
随 的增大而增大,
的增大而增大,
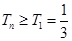 11分
11分
又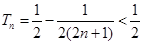 12分
12分
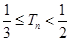 . 13分
. 13分
考点:(1)数列的通项公式;(2)裂项相消法求数列的和,数列的单调性与不等式的证明.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 ?
? 是公差不为零的等差数列,
是公差不为零的等差数列,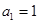 ,且
,且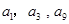 成等比数列.
成等比数列.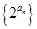 的前
的前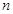 项和
项和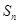 .
.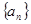 的前n项的和
的前n项的和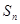 与
与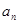 的关系是
的关系是 .
.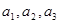 并归纳出数列
并归纳出数列 的前
的前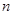 项和
项和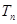 .
. 的相邻两项
的相邻两项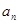 ,
,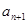 是关于
是关于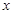 方程
方程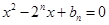 的两根,且
的两根,且 .
.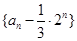 是等比数列;
是等比数列;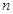 项和
项和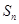 ;
;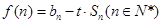 ,若
,若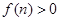 对任意的
对任意的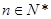 都成立,求实数
都成立,求实数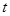 的取值范围.
的取值范围.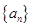 的前n项和为
的前n项和为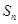 ,且
,且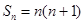 ,数列
,数列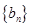 满足
满足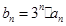 .
.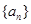 的前
的前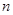 项和
项和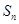 满足
满足 ,
,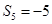 。
。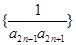 的前
的前 }的前
}的前 项和
项和 ,则其通项
,则其通项 ;
; 项满足
项满足 ,则
,则