题目内容
( 13分)设函数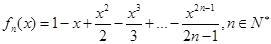
(1)研究函数 的单调性;
的单调性;
(2)判断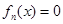 的实数解的个数,并加以证明.
的实数解的个数,并加以证明.
【答案】
(1) 在
在 单调递减.
单调递减.
(2) 有唯一实数解.
有唯一实数解.
【解析】解:(1)
所以 在
在 单调递减.……………………………………4分
单调递减.……………………………………4分
(2) 有唯一实数解
有唯一实数解 .
.
由 ,及
,及 在
在 单调递减,
单调递减,
知 在
在 有唯一实数解,从而
有唯一实数解,从而 在
在 有唯一实数解.
有唯一实数解.
推断 在
在 有唯一实数解
有唯一实数解
当 时,由
时,由 ,得
,得

(i)若 ,则
,则
(ii)
若 ,则
,则
(iii)
若 且
且 时,则
时,则
① 当 时,
时,
② 当 时,
时,
综合i, ii, iii,得 ,即
,即 在
在 单调递减……………10分
单调递减……………10分
 >0,又
>0,又


 <0 ……………12分
<0 ……………12分
所以 在
在 有唯一实数解,从而
有唯一实数解,从而 在
在 有唯一实数解.
有唯一实数解.
综上, 有唯一实数解.……………………………………………13分
有唯一实数解.……………………………………………13分

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 对任意的实数
对任意的实数 ,都有
,都有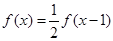 ,且当
,且当 时,
时, 。
。 时,求
时,求 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点 ,使得函数在点
,使得函数在点 平行。若存在,那么这样的点
平行。若存在,那么这样的点 ,且
,且  ,记
,记 ,求证:
,求证:  。
。 ,已知
,已知 ,且
,且 ,曲线
,曲线 在x=1处取极值.
在x=1处取极值. 的递增区间为
的递增区间为 ,求
,求 的取值范围;
的取值范围;
 是与
是与 无关的常数
无关的常数 时,恒有
时,恒有 ,求实数
,求实数 的最小值
的最小值