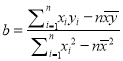Question

【题目】已知二次函数(是常数，且)满足条件：，且方程有两个相等实根．

(1)求的解析式；

(2)是否存在实数，使的定义域和值域分别为和？若存在，求出的值；若不存在，说明理由．

Answer 1

【答案】(1) f(x)＝－x2＋x；（2）m＝－2，n＝0.

【解析】

(1)方程　f(x)＝x，即ax2＋bx＝x，

亦即ax2＋(b－1)x＝0，

由方程有两个相等实根，得Δ＝(b－1)2－4a×0＝0，

∴b＝1.①

由f(2)＝0，得4a＋2b＝0②

由①、②得，a＝－，b＝1，

故　f(x)＝－x2＋x.

(2)假设存在实数m、n满足条件，由(1)知，

　f(x)＝－x2＋x＝－(x－1)2＋≤，

则2n≤，即n≤.

∵　f(x)＝－(x－1)2＋的对称轴为x＝1，

∴当n≤时，　f(x)在[m，n]上为增函数．

于是有即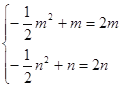

∴m<n≤，∴.

故存在实数m＝－2，n＝0，

使f(x)的定义域为[m，n]，值域为[2m,2n]．