题目内容
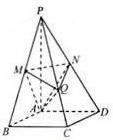 (2012•浙江)如图,在四棱锥P-ABCD中,底面是边长为2
(2012•浙江)如图,在四棱锥P-ABCD中,底面是边长为2| 3 |
| 6 |
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角A-MN-Q的平面角的余弦值.
分析:(1)连接BD,利用三角形的中位线的性质,证明MN∥BD,再利用线面平行的判定定理,可知MN∥平面ABCD;
(2)方法一:连接AC交BD于O,以O为原点,OC,OD所在直线为x,y轴,建立空间直角坐标系,求出平面AMN的法向量
=(2
,0,-1),利用向量的夹角公式,即可求得二面角A-MN-Q的平面角的余弦值;
方法二:证明∠AEQ为二面角A-MN-Q的平面角,在△AED中,求得AE=
,QE=
,AQ=2
,再利用余弦定理,即可求得二面角A-MN-Q的平面角的余弦值.
(2)方法一:连接AC交BD于O,以O为原点,OC,OD所在直线为x,y轴,建立空间直角坐标系,求出平面AMN的法向量
| m |
| 2 |
方法二:证明∠AEQ为二面角A-MN-Q的平面角,在△AED中,求得AE=
3
| ||
| 2 |
| ||
| 2 |
| 2 |
解答:(1)证明:连接BD.∵M,N分别为PB,PD的中点,
∴在△PBD中,MN∥BD.
又MN?平面ABCD,BD?平面ABCD
∴MN∥平面ABCD;
(2)方法一:连接AC交BD于O,以O为原点,OC,OD所在直线为x,y轴,建立空间直 角坐标系,在菱形ABCD中,∠BAD=120°
角坐标系,在菱形ABCD中,∠BAD=120°
,得AC=AB=2
,BD=
AB=6
∵PA⊥平面ABCD,∴PA⊥AC
在直角△PAC中,AC=2
,PA=2
,AQ⊥PC得QC=2,PQ=4,由此知各点坐标如下
A(-
,0,0),B(0,-3,0),C(
,0,0),D(0,3,0),P(-
,0,2
),M(-
,-
,
),N(-
,
,
)
Q(
,0,
)
设
=(x,y,z)为平面AMN的法向量,则
=(
,-
,
),
=(
,
,
).
∴
,取z=-1,
=(2
,0,-1),
同理平面QMN的法向量为
=(2
,0,5)
∴cos<
,
> =
=
∴所求二面角A-MN-Q的平面角的余弦值为
.
方法二:在菱形ABCD中,∠BAD=120°,得AC=AB=BC=CD=DA=2
,BD=
AB=6
∵PA⊥平面ABCD,∴PA⊥AB,PA⊥AC,PA⊥AD,∴PB=PC=PD,∴△PBC≌△PDC
而M,N分别是PB,PD的中点,∴MQ=NQ,且AM=
PB=
PD=AN
取MN的中点E,连接AE,EQ,则AE⊥MN,QE⊥MN,所以∠AEQ为二面角A-MN-Q的平面角
由AB=2
,PA=2
,AM=AN=3,MN=3可得AE=
在直角△PAC中,AQ⊥PC得QC=2,PQ=4,AQ=2
在△PBC中,cos∠BPC=
,∴MQ=
=
在等腰△MQN中,MQ=NQ=
.MN=3,∴QE=
在△AED中,AE=
,QE=
,AQ=2
,∴cos∠AEQ=
∴所求二面角A-MN-Q的平面角的余弦值为
.
∴在△PBD中,MN∥BD.
又MN?平面ABCD,BD?平面ABCD
∴MN∥平面ABCD;
(2)方法一:连接AC交BD于O,以O为原点,OC,OD所在直线为x,y轴,建立空间直
 角坐标系,在菱形ABCD中,∠BAD=120°
角坐标系,在菱形ABCD中,∠BAD=120°,得AC=AB=2
| 3 |
| 3 |
∵PA⊥平面ABCD,∴PA⊥AC
在直角△PAC中,AC=2
| 3 |
| 6 |
A(-
| 3 |
| 3 |
| 3 |
| 6 |
| ||
| 2 |
| 3 |
| 2 |
| 6 |
| ||
| 2 |
| 3 |
| 2 |
| 6 |
Q(
| ||
| 3 |
2
| ||
| 3 |
设
| m |
| AM |
| ||
| 2 |
| 3 |
| 2 |
| 6 |
| AN |
| ||
| 2 |
| 3 |
| 2 |
| 6 |
∴
|
| m |
| 2 |
同理平面QMN的法向量为
| n |
| 2 |
∴cos<
| m |
| n |
| ||||
|
|
| ||
| 33 |
∴所求二面角A-MN-Q的平面角的余弦值为
| ||
| 33 |
方法二:在菱形ABCD中,∠BAD=120°,得AC=AB=BC=CD=DA=2
| 3 |
| 3 |
∵PA⊥平面ABCD,∴PA⊥AB,PA⊥AC,PA⊥AD,∴PB=PC=PD,∴△PBC≌△PDC
而M,N分别是PB,PD的中点,∴MQ=NQ,且AM=
| 1 |
| 2 |
| 1 |
| 2 |
取MN的中点E,连接AE,EQ,则AE⊥MN,QE⊥MN,所以∠AEQ为二面角A-MN-Q的平面角
由AB=2
| 3 |
| 6 |
3
| ||
| 2 |
在直角△PAC中,AQ⊥PC得QC=2,PQ=4,AQ=2
| 2 |
在△PBC中,cos∠BPC=
| 5 |
| 6 |
| PM2+PQ2-2PM•PQcos∠BPC |
| 5 |
在等腰△MQN中,MQ=NQ=
| 5 |
| ||
| 2 |
在△AED中,AE=
3
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 33 |
∴所求二面角A-MN-Q的平面角的余弦值为
| ||
| 33 |
点评:本题考查线面平行,考查面面角,解题的关键是利用线面平行的判定定理,掌握面面角的两种求解方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•浙江)如图,椭圆C:
(2012•浙江)如图,椭圆C: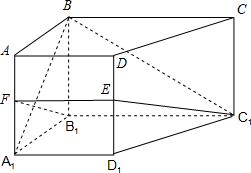 (2012•浙江)如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=
(2012•浙江)如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=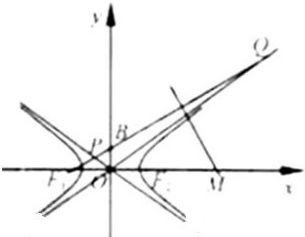 (2012•浙江)如图,F1,F2分别是双曲线C:
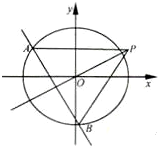
(2012•浙江)如图,F1,F2分别是双曲线C: (2012•浙江)如图,在直角坐标系xOy中,点P(1,
(2012•浙江)如图,在直角坐标系xOy中,点P(1,