题目内容
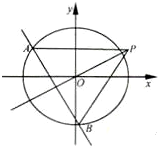 (2012•浙江)如图,椭圆C:
(2012•浙江)如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 10 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求△APB面积取最大值时直线l的方程.
分析:(Ⅰ)由题意,根据离心率为
,其左焦点到点P(2,1)的距离为
,建立方程,即可求得椭圆C的方程;
(Ⅱ)设A(x1,y1),B(x2,y2),线段AB的中点为M,当AB⊥x轴时,直线AB的方程为x=0,与不过原点的条件不符,故设AB的方程为y=kx+m(m≠0)由
,消元再利用韦达定理求得线段AB的中点M,根据M在直线OP上,可求|AB|,P到直线AB的距离,即可求得△APB面积,从而问题得解.
| 1 |
| 2 |
| 10 |
(Ⅱ)设A(x1,y1),B(x2,y2),线段AB的中点为M,当AB⊥x轴时,直线AB的方程为x=0,与不过原点的条件不符,故设AB的方程为y=kx+m(m≠0)由
|
解答:解:(Ⅰ)由题意
,解得:
.
∴所求椭圆C的方程为:
+
=1.
(Ⅱ)设A(x1,y1),B(x2,y2),线段AB的中点为M
当AB⊥x轴时,直线AB的方程为x=0,与不过原点的条件不符,故设AB的方程为y=kx+m(m≠0)
由
,消元可得(3+4k2)x2+8kmx+4m2-12=0①
∴x1+x2=-
,x1x2=
∴线段AB的中点M( -
,
)
∵M在直线OP上,∴-
=
∴k=-
故①变为3x2-3mx+m2-3=0,又直线与椭圆相交,
∴△>0,x1+x2=m,x1x2=
∴|AB|=
×
P到直线AB的距离d=
∴△APB面积S=
|AB|d=
×
(m∈(-2
,0)∪(0,2
)
令u(m)=(12-m2)(m-4)2,则u′(m)=-4(m-4)(m-1-
)(m-1+
)
∴m=1-
,u(m)取到最大值
∴m=1-
时,S取到最大值
综上,所求直线的方程为:3x+2y+2
-2=0
|
|
∴所求椭圆C的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设A(x1,y1),B(x2,y2),线段AB的中点为M
当AB⊥x轴时,直线AB的方程为x=0,与不过原点的条件不符,故设AB的方程为y=kx+m(m≠0)
由
|
∴x1+x2=-
| 8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
∴线段AB的中点M( -
| 4km |
| 3+4k2 |
| 3m |
| 3+4k2 |
∵M在直线OP上,∴-
| 2km |
| 3+4k2 |
| 3m |
| 3+4k2 |
∴k=-
| 3 |
| 2 |
故①变为3x2-3mx+m2-3=0,又直线与椭圆相交,
∴△>0,x1+x2=m,x1x2=
| m2-3 |
| 3 |
∴|AB|=
| ||
| 6 |
| 12-m2 |
P到直线AB的距离d=
| 2|m-4| | ||
|
∴△APB面积S=
| 1 |
| 2 |
| ||
| 6 |
| (m-4)2(12-m2) |
| 3 |
| 3 |
令u(m)=(12-m2)(m-4)2,则u′(m)=-4(m-4)(m-1-
| 7 |
| 7 |
∴m=1-
| 7 |
∴m=1-
| 7 |
综上,所求直线的方程为:3x+2y+2
| 7 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查导数知识的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
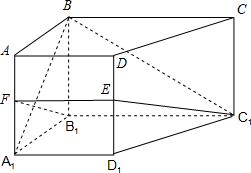 (2012•浙江)如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=
(2012•浙江)如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=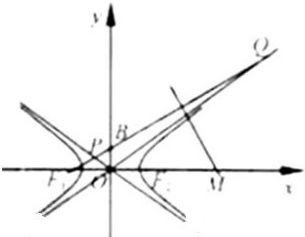 (2012•浙江)如图,F1,F2分别是双曲线C:
(2012•浙江)如图,F1,F2分别是双曲线C: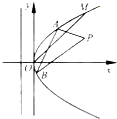 (2012•浙江)如图,在直角坐标系xOy中,点P(1,
(2012•浙江)如图,在直角坐标系xOy中,点P(1,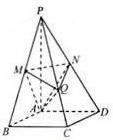 (2012•浙江)如图,在四棱锥P-ABCD中,底面是边长为
(2012•浙江)如图,在四棱锥P-ABCD中,底面是边长为