题目内容
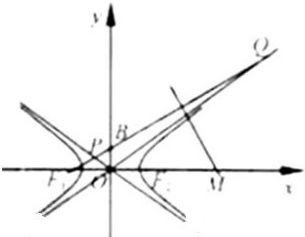 (2012•浙江)如图,F1,F2分别是双曲线C:
(2012•浙江)如图,F1,F2分别是双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
分析:确定PQ,MN的斜率,求出直线PQ与渐近线的交点的坐标,得到MN的方程,从而可得M的横坐标,利用|MF2|=|F1F2|,即可求得C的离心率.
解答:解:|OB|=b,|O F1|=c.∴kPQ=
,kMN=-
.
直线PQ为:y=
(x+c),两条渐近线为:y=±
x.
由
,得Q(
,
);由
得P(
,
).
∴直线MN为y-
=-
(x-
),
令y=0得:xM=c(1+
).
又∵|MF2|=|F1F2|=2c,
∴3c=xM=c(1+
),
∴3a2=2c2
解之得:e2=
,即e=
.
故选B.
| b |
| c |
| c |
| b |
直线PQ为:y=
| b |
| c |
| b |
| a |
由
|
| ac |
| c-a |
| bc |
| c-a |
|
| -ac |
| c+a |
| bc |
| c+a |
∴直线MN为y-
| bc2 |
| c2-a2 |
| c |
| b |
| a2c |
| c2-a2 |
令y=0得:xM=c(1+
| a2 |
| b2 |
又∵|MF2|=|F1F2|=2c,
∴3c=xM=c(1+
| a2 |
| b2 |
∴3a2=2c2
解之得:e2=
| 3 |
| 2 |
| ||
| 2 |
故选B.
点评:本题考查双曲线的几何形状,考查解方程组,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
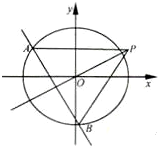 (2012•浙江)如图,椭圆C:
(2012•浙江)如图,椭圆C: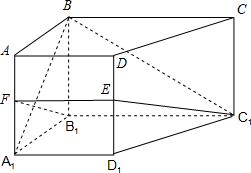 (2012•浙江)如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=
(2012•浙江)如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=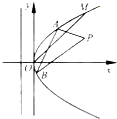 (2012•浙江)如图,在直角坐标系xOy中,点P(1,
(2012•浙江)如图,在直角坐标系xOy中,点P(1,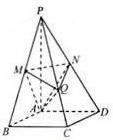 (2012•浙江)如图,在四棱锥P-ABCD中,底面是边长为
(2012•浙江)如图,在四棱锥P-ABCD中,底面是边长为