Question

3．某学校要举办体育节，同时确定在高一年级一班学生中选拔仪仗队员．该班首先侧量了本班学生的身高，并把所得数据按照区间：[150，160），[160，170），[170，180），[180，190]（单位：cm）分组，分别得到了男生和女生的频率分布直方图，如图所示，其中男生（图1）在区间[160，170）内的人数是6人，女生（图2）在区间[160，170）内的人数是15人．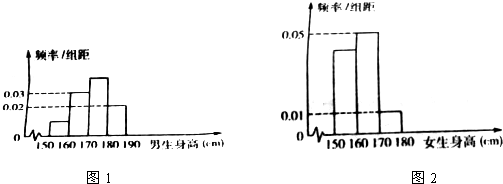

（1）该班共有多少学生？
（2）要从身高180cm以上（含180）的男生中选拔两名旗手，从身高170cm以上（含170）的女生中选拔两名旗手，求男生甲（身高在180cm以上）和女生乙（身高在170cm以上）同时当选的概率．

Answer 1

分析 （1）利用男生和女生的频率分布直方图，得出相应的频率，即可求出学生数；
（2）身高180cm以上（含180）的男生，有4人，身高170cm以上（含170）的女生，有3人，选拔两名旗手，有${C}_{7}^{2}$=21种情况，即可求男生甲（身高在180cm以上）和女生乙（身高在170cm以上）同时当选的概率．

解答 解：（1）∵男生（图1）在区间[160，170）内的人数是6人，女生（图2）在区间[160，170）内的人数是15人．
∴男生有$\frac{6}{0.3}$=20人，女生有$\frac{15}{0.5}$=30人，
∴该班共有50学生；
（2）身高180cm以上（含180）的男生，有4人，身高170cm以上（含170）的女生，有3人，选拔两名旗手，有${C}_{7}^{2}$=21种情况，
∴男生甲（身高在180cm以上）和女生乙（身高在170cm以上）同时当选的概率为$\frac{1}{21}$．

点评 本题考查频率分布直方图，考查概率的计算，正确理解频率分布直方图是关键．