题目内容
已知函数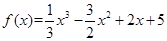 .
.
(Ⅰ)求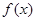 的单调区间;
的单调区间;
(Ⅱ)若曲线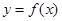 与
与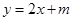 有三个不同的交点,求实数
有三个不同的交点,求实数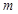 的取值范围.
的取值范围.
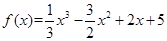 .
.(Ⅰ)求
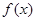 的单调区间;
的单调区间;(Ⅱ)若曲线
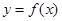 与
与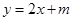 有三个不同的交点,求实数
有三个不同的交点,求实数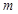 的取值范围.
的取值范围.(Ⅰ) 单调递增区间为 ,单调递减区间为
,单调递减区间为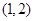 ;(Ⅱ)
;(Ⅱ)  .
.
 ,单调递减区间为
,单调递减区间为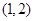 ;(Ⅱ)
;(Ⅱ)  .
.试题分析:(Ⅰ)先对函数求导得
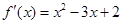 ,然后求出导函数的零点,讨论零点所分区间上导函数的正负,以此来判断函数的单调性,导数为正的区间是对应函数的递增区间,导数为负的区间是对应函数的递减区间;(Ⅱ)先化简
,然后求出导函数的零点,讨论零点所分区间上导函数的正负,以此来判断函数的单调性,导数为正的区间是对应函数的递增区间,导数为负的区间是对应函数的递减区间;(Ⅱ)先化简 得到
得到 ,然后构造函数
,然后构造函数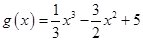 ,将问题转化为“函数
,将问题转化为“函数 与
与 有三个公共点”.由数形结合的思想可知,当
有三个公共点”.由数形结合的思想可知,当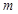 在函数
在函数 的两个极值点对应的函数值之间时,函数
的两个极值点对应的函数值之间时,函数 与
与 有三个公共点,那么只要利用函数
有三个公共点,那么只要利用函数 的导数找到此函数的两个极值即可.
的导数找到此函数的两个极值即可.试题解析:(Ⅰ)
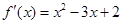 2分
2分令
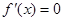 ,解得
,解得 或
或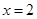 . 4分
. 4分当
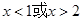 时,
时, ;当
;当 时,
时,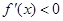
∴
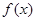 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为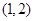 6分
6分(Ⅱ)令
 ,即
,即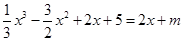
∴

设

 ,即考察函数
,即考察函数 与
与 何时有三个公共点 8分
何时有三个公共点 8分令
 ,解得
,解得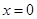 或
或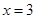 .
.当
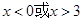 时,
时,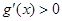
当
 时,
时,
∴
 在
在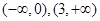 单调递增,在
单调递增,在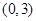 单调递减 9分
单调递减 9分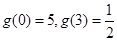 10分
10分根据图象可得
 . 12分
. 12分
练习册系列答案
相关题目
 ,恒过定点
,恒过定点 .
. ;
; 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 ,设函数
,设函数 ,直接写出
,直接写出 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.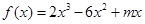
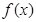 的解析表达式;
的解析表达式;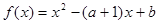 ,
,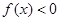 的解集是
的解集是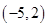 ,求
,求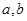 的值;
的值;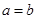 ,解关于
,解关于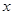 的不等式
的不等式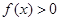 .
.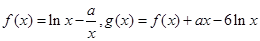 ,其中
,其中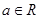 .
.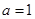 时判断
时判断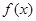 的单调性;
的单调性;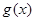 在其定义域为增函数,求正实数
在其定义域为增函数,求正实数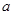 的取值范围;
的取值范围;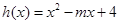 ,当
,当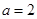 时,若
时,若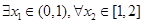 ,总有
,总有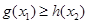 成立,求实数
成立,求实数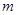 的取值范围.
的取值范围.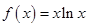 .
.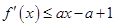 恒成立,求实数a的集合.
恒成立,求实数a的集合. 在点
在点 的切线方程是____________
的切线方程是____________ 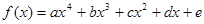 ,
,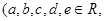 且
且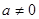 )的四个零点构成公差为2的等差数列,则
)的四个零点构成公差为2的等差数列,则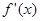 的所有零点中最大值与最小值之差是( )
的所有零点中最大值与最小值之差是( )


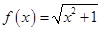 ,对任意
,对任意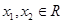 ,恒有
,恒有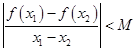 ,其中M是常数,则M的最小值是 .
,其中M是常数,则M的最小值是 .