题目内容
飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东30°,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s.(1)求A、C两个救援中心的距离;
(2)求在A处发现P的方向角;
(3)若信号从P点的正上方Q点处发出,则A、B收到信号的时间差变大还是变小,并证明你的结论.
分析:(1)首先以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,求出A,B,C的坐标,然后求出AC的距离即可.
(2)根据|PC|=|PB|得出P在BC线段的垂直平分线上,建立双曲线方程,并求出∠PAB.
(3)设|PQ|=h,|PB|=x,|PA|=y,建立不等式,并求解,得到A、B收到信号的时间差变小
(2)根据|PC|=|PB|得出P在BC线段的垂直平分线上,建立双曲线方程,并求出∠PAB.
(3)设|PQ|=h,|PB|=x,|PA|=y,建立不等式,并求解,得到A、B收到信号的时间差变小
解答: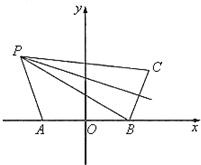
 解:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,
解:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,
则A(-3,0),B(3,0),C(5,2
)
则|AC|=
=2
km
即A、C两个救援中心的距离为2
km
(2)∵|PC|=|PB|,所以P在BC线段的垂直平分线上
又∵|PB|-|PA|=4,所以P在以A、B为焦点的双曲线的左支上,且|AB|=6
∴双曲线方程为
-
=1 (x<0)
BC的垂直平分线的方程为x+
y-7=0
联立两方程解得:x=-8∴P(-8,5
),kPA=tan∠PAB=-
∴∠PAB=120°所以P点在A点的北偏西30°处
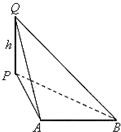 (3)如图,设|PQ|=h,|PB|=x,|PA|=y
(3)如图,设|PQ|=h,|PB|=x,|PA|=y
∵|QB|-|QA|=
-
=
=(x-y)•
又∵
<1
∴|QB|-|QA|<|PB|-|PA|∴
-
<
-
即A、B收到信号的时间差变小

 解:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,
解:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,则A(-3,0),B(3,0),C(5,2
| 3 |
则|AC|=
(5+3)2+(2
|
| 19 |
即A、C两个救援中心的距离为2
| 19 |
(2)∵|PC|=|PB|,所以P在BC线段的垂直平分线上
又∵|PB|-|PA|=4,所以P在以A、B为焦点的双曲线的左支上,且|AB|=6
∴双曲线方程为
| x2 |
| 4 |
| y2 |
| 5 |
BC的垂直平分线的方程为x+
| 3 |
联立两方程解得:x=-8∴P(-8,5
| 3 |
| 3 |
∴∠PAB=120°所以P点在A点的北偏西30°处
 (3)如图,设|PQ|=h,|PB|=x,|PA|=y
(3)如图,设|PQ|=h,|PB|=x,|PA|=y∵|QB|-|QA|=
| x2+h2 |
| y2+h2 |
=
| x2-y2 | ||||
|
| x+y | ||||
|
又∵
| x+y | ||||
|
∴|QB|-|QA|<|PB|-|PA|∴
| |QB| |
| 1 |
| |QA| |
| 1 |
| |PB| |
| 1 |
| |PA| |
| 1 |
即A、B收到信号的时间差变小
点评:本题考查双曲线方程的应用,涉及到解空间几何体的方法,通过对双曲线知识与立体几何知识的糅合,考查学生对知识的应用能力,属于中档题.

练习册系列答案
相关题目
 某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.
某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.

