题目内容
如图,已知圆A:(x+3)2+y2=100,圆A内一定点B(3,0),动圆P过B点且与圆A内切,求圆心P的轨迹方程.
解:设|PB|=r.
∵圆P与圆A内切,圆A的半径为10,
∴两圆的圆心距|PA|=10-r,
即|PA|+|PB|=10(大于|AB|).
∴点P的轨迹是以A、B两点为焦点的椭圆.
∴2a=10,2c=|AB|=6.
∴a=5,c=3.
∴b2=a2-c2=25-9=16,
即点P的轨迹方程为![]() +
+![]() =1.
=1.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
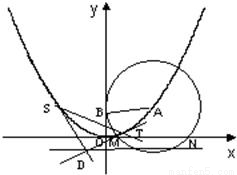
 如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为圆A在x轴上所截得的弦.
如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为圆A在x轴上所截得的弦.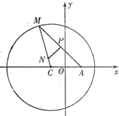 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足 (2010•重庆三模)如图,已知圆G:
(2010•重庆三模)如图,已知圆G: (2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3椭圆D:
(2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3椭圆D: