题目内容
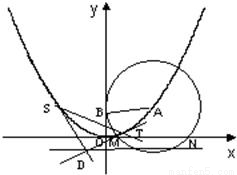
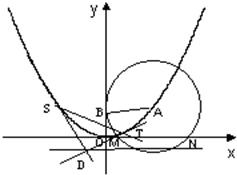 如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为圆A在x轴上所截得的弦.
如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为圆A在x轴上所截得的弦.(Ⅰ)证明:|MN|是定值;
(Ⅱ)讨论抛物线C的准线l与圆A的位置关系;
(Ⅲ)设D是抛物线C的准线l上任意一点,过D向抛物线作两条切线DS,DT(切点是S,T),判断直线ST是否过定点,并证明你的结论.
分析:(Ⅰ)设A(x0,y0),根据抛物线的方程求得其横坐标和纵坐标的关系,根据两点间的距离表ishichu圆的半径,进而表示出圆的方程,把y=0,和x02=4y0代入,表示出x1和x2进而求得|MN|为定值.
(Ⅱ)先表示出圆心A到抛物线准线方程的距离,进而表示出d2-r2,根据y0的范围确定抛物线与圆的位置关系.
(Ⅲ)设出切点的坐标,对抛物线方程求导,求得切点处直线的斜率,表示出切线方程,把切点代入求得x1x2,进而根据S,T坐标表示出直线方程,把x1x2的值代入,进而根据直线的方程推断出直线恒过定点(0,1).
(Ⅱ)先表示出圆心A到抛物线准线方程的距离,进而表示出d2-r2,根据y0的范围确定抛物线与圆的位置关系.
(Ⅲ)设出切点的坐标,对抛物线方程求导,求得切点处直线的斜率,表示出切线方程,把切点代入求得x1x2,进而根据S,T坐标表示出直线方程,把x1x2的值代入,进而根据直线的方程推断出直线恒过定点(0,1).
解答: 解:(Ⅰ)设A(x0,y0),则x02=4y0,
解:(Ⅰ)设A(x0,y0),则x02=4y0,
则圆A的半径r=|AB|=
,
则圆A的方程为(x-x0)2+(y-y0)2=x02+(y0-2)2,
令y=0,并将x02=4y0代入得x2-2x0x+x02-4=0,
解得x1=x0-2,x2=x0+2,∴|MN|=|x1-x2|=4为定值.
(Ⅱ)圆心A到抛物线准线l:y=-1的距离为d=y0+1,
则d2-r2=6y0-3-x02=2y0-3
所以,当0≤y0<
时,d<r,抛物线C的准线l与圆A相交;
当y0=
时,d=r,抛物线C的准线l与圆A相切;
当y0>
时,d=r,抛物线C的准线l与圆A相离.
(Ⅲ)设切点为S(x1,
),T(x2,
),由y′=
xk,
则切线为y+1=
(x-t),
所以
=
xkt+1,(k=1,2)?消去t可得,x1x2=-4.
又kST=
=
,
所以直线ST的方程是y-
=
(x-x1),
即y=
x-
,
把x1x2=-4,代入得y=
x+1,
故直线ST是过定点F(0,1).
 解:(Ⅰ)设A(x0,y0),则x02=4y0,
解:(Ⅰ)设A(x0,y0),则x02=4y0,则圆A的半径r=|AB|=
|
则圆A的方程为(x-x0)2+(y-y0)2=x02+(y0-2)2,
令y=0,并将x02=4y0代入得x2-2x0x+x02-4=0,
解得x1=x0-2,x2=x0+2,∴|MN|=|x1-x2|=4为定值.
(Ⅱ)圆心A到抛物线准线l:y=-1的距离为d=y0+1,
则d2-r2=6y0-3-x02=2y0-3
所以,当0≤y0<
| 3 |
| 2 |
当y0=
| 3 |
| 2 |
当y0>
| 3 |
| 2 |
(Ⅲ)设切点为S(x1,
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
则切线为y+1=
| xk |
| 2 |
所以
| ||
| 4 |
| 1 |
| 2 |
又kST=
| x12-x22 |
| 4(x1-x2) |
| x1+x2 |
| 4 |
所以直线ST的方程是y-
| ||
| 4 |
| x1+x2 |
| 4 |
即y=
| x1+x2 |
| 4 |
| x1x2 |
| 4 |
把x1x2=-4,代入得y=
| x1+x2 |
| 4 |
故直线ST是过定点F(0,1).
点评:本题主要考查了抛物线的应用.考查了考生综合运用基础知识的能力.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目